Place Value Worksheets
We are beginning to work with large numbers by the time that we have reached this section. Since we follow the decimal system, which is built up from the base ten system, each position in number is ten times greater or less than the number to the right or left of it. To determine the value of integer located with in a number start by locating the decimal point. The integer located directly to the left of decimal point is the ones place. This is our foundation to work off of. As we move to the integer to the left of the ones place each integer is ten times greater than the previous location. As we move to the right each position is ten times less than the previous value. As you move to the right of the decimal those integers indicate fractional values. You will find a wide range of worksheets and lessons below to help you better understand this concept. This is a skill that I feel is covered well on my site. If you know of anything I am missing, please let me know.
- Comparing Multi-Digit Numbers - Students learn how to compare the values of integers found within numbers.
- Compare Two Decimals (to the hundredths place) - We look at specific integers found within numbers and compare them.
- Decimals in Numeric, Word, and Expanded Form - We look at all the formats a decimal value can be displayed in and show students how to express those values.
- Forms of Numbers (Numerals, Number Names, Expanded Form) - Students learn a great deal about the how to communicate values.
- Identifying Place Values with Decimals - It is all about where the decimal point lies.
- Identifying Place Values within Numbers - These are whole numbers that do not contain a decimal.
- Identifying Whole Number Place Values (Up to Hundred Thousand) - This helps students transition to using the expanded form of numbers.
- Naming Numbers - Time to match words to numbers. This is where math and language meet for the first time.
- Ones and Tens Place Value Blocks - A visual way of looking at these smaller place values.
- Ones, Tens, Hundreds, and Thousands Blocks - We expanded to larger values. A really good way to lock in the concept.
- One and Tens Place Values - The smallest of values are front and center in this section.
- Place Value (Ones, Tens, Hundreds) - We start to spring load these values. Students learn that each successive place jumps by powers of ten.
- Place Value: Understanding How to Round Decimals - It is based on the previous place that came your way.
- Place Value and the Expanded Form of Numbers - Students rarely understand that values less than one can be expressed in expanded form.
- Place Value Rearrangement - How do we move the integers around to make the largest or smallest value?
- Place Values and Ten Times Differences - We look at the concept of powers of ten.
- Rounding Numbers By Place Value - As usually we are looking for an integer of five or greater to raise value otherwise, we drop the value.
- Ten More Or Ten Less - This is just like skip counting we pivot in packets of ten. The is the key concept behind the base ten system.
- The Tens, Hundred, and Thousands Place - What is the significance of each value within each of these integers?
- Writing Names of Numbers and Expanded Format - We name numbers based on their place value and express this through writing values in expanded form.
What are Place Values?
The place value system tells us that the position of a digit within a number determines its value. The numbers that we come across all our lives will have no meaning without place values. When studying number systems, understanding the concept of place values is extremely crucial. It is important to remember that every digit in a number has a unique place value, which gives it a meaning.
The entire system is based on the base ten or decimal system. This simply indicates that each position you move is ten times less than or ten times greater than the position you just moved from. As we move to the left the values are ten times greater than the previous place. As we move to the right the values are ten times less than the previous position.
The smallest non-fractional place value is the ones place, and it is followed by tens, hundreds, thousands, so on and so forth. The numbers on the right side of the decimal point are fractional values that are less than one whole unit. They have the place values starting with the tenth, hundredth, thousandth, so on and so forth.
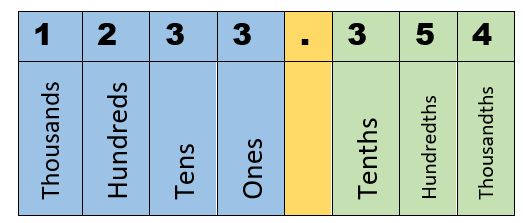
Consider a number 1233.354
Left side of the Decimal | 1st digit: 1 here represents one thousand | 2nd digit: 2 here represents two hundred | 3rd digit: 3 here represents three tens 4th digit: 3 here represents three units
Right side of the Decimal | 1st digit: 3 here represents 3/10 | 2nd digit: 5 here represents 5/100 | 3rd digit: 4 here represents 4/1000
Below is a full value breakdown of the number visualized for you. The whole number values have a blue backdrop, and the decimal values have a green backdrop.
Why Is This Concept Important?
This is a fundamental aspect of math and students often find the concept abstract, at first. Recognizing the significance of each digit within a number helps you completely understand the meaning of the overall value. It gives each digit purpose and standing within the overall value itself. When students learn to process math operations, outside of the scope of their math facts, place value is significant. The concept of regrouping and borrowing is built entire upon understanding the concept of a digits value within an integer. As students learn more about the base-ten system, this is the starting point that will lead them towards all types of applications within it. The best way to approach this concept with students is to work with the good old ones and tens blocks. Once they have a concrete understanding, then you can put it on paper and help them see that each successive value to the left is ten times greater than the previous digit. It helps to demonstrate this concept to students by helping students learn to convert between standard and expanded form. They quickly learn that each value is ten times greater than the previous one. As your students transition to using decimal value, this makes it easy to explain because all the digits are ten times greater or lesser than one another, just in a different direction. This will pop up again as you move it to financial and scientific forms of notation. This concept will follow you well into high school and college for certain.