Ratios and Proportion Worksheets
Many students and even adults that have not been around math for a while often get these two distinct concepts confused. Ratios are used to compare two values. The integers that are used tell us how much of one thing we have compared to another. There are several different ways in which they are stated. Over the series of these topics, we go over each of them. Proportions is a math statement that indicates that two ratios are equal. Know that these things are equal allows us to scale things by making them bigger or smaller quickly and easily. The worksheets and lessons that you will find below will not only learn skills of these topic, but also how they can be applied to the real world.
- Equivalent Ratios - We show you not only how recognize them, but also to generate them.
- Graphs of Proportional Relationships - We begin to show students how to distinguish trends on graphs.
- Gratuities and Commissions, Fees, and Tax - Students learn how to determine many real-world finance issues.
- Markups and Markdowns Word Problems - Students begin to understand how this skews pricing and we hint to the concept of margins.
- Multistep Ratio and Percent Word Problems - Hope you brushed up on your cross multiplication.
- Percentage as a Rate per Hundred - You basically just drop the percentage value over a fraction of one hundred.
- Percent Error and Percent Increase - This helps us gauge how fast the value is jumping up and falling.
- Proportional Relationships Word Problems - We help make sense of data you will find in these problems.
- Ratio and Rates Word Problems - We start to see how ratios relate to rates of change and how fast they accelerate.
- Ratios and Units of Measurement - We often forget that units of measure are just as important as the values that they represent.
- Recognizing Proportional Relationships - How to spot them and interpret what that means to you.
- Tape Diagrams / Bar Models - We introduce you a method you can use to visualize a ratio.
- What is a Ratio? - The most general introduction to the topic.
- The Constant of Proportionality - This is the ratio value that exists between two directly proportional values.
- Unit Rates and Ratios of Fractions - We show you how the two interconnect and can be used to your advantage.
- Unit Rates and Ratios : The Relationship - A slight better way to visualize and make sense of the topic.
- Unit Rates with Speed and Price Word Problems - The unit price truly indicates if you are getting a deal comparatively.
What are Ratios?
To compare values, we use the concept of ratios. When we use the term, "to," write two numbers as a fraction, or with a colon between them, we are representing a ratio. It is a comparison of the quantities of two things. It is a measure of how much of thing is there, in comparison to another thing.
A ratio can be used to represent a comparison between two things, and we call it part-to-part ratios. There are cases when you have to compare a part to a whole lot, and we call these ratios part-to-whole. The concept of ratios is very commonly used in writing down recipes.
Example: A delegation comprising of five pupils was sent to XYZ college to represent a school. Out of these five, three were female, and two were male pupils.
We can represent this information in the form of two ratios; part-to-part and whole-to-part.
Part-to-Part: - The ratio of females to male can be written as 3:2 or 3/2 The ratio of males to females can be written as 2:3 or 2/3
Whole-to-Part: - The ratio of females to the whole delegation can be written as 3:5 or 3/5 The ratio of males to the whole delegation can be written as 2:5 or 2/5
This really gets hot right around the middle grade levels. These skills are used endless throughout life, so it is important for students to grasp this.
What are Proportions?
Proportions are equations that state that two ratios are equivalent. If we know that we have a equivalent ratios it allows us to scale things up in size or quantity very quickly. There will be times where you will need to evaluate the truth of proportions. If they are equal ratios, they are true. If they are not equal, they are false. We can use proportions to help solve all types of unit rate based problems.

Example: Jennifer travels in a car at a constant speed of 60 miles per hour from Boston to Quebec City. The distance between the two cities is 300 miles. How long does it take her?
Solution: We know that we have a proportion of 60 miles per 1 hour. We want to know the equivalent proportion that would travel 300 miles. The math would look like this:
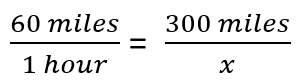
We would then cross multiply to rearrange the portion as: 300 = 60x
We would divide both sides by 60 and be left with 5 = x.
This means it would take 5 hours to travel that distance.
What is The Difference Between a Ratio and a Proportion?
Ratios are used to compare two quantities. This comparison is made by using the division operation. They are written in form a/b. Proportions are equations that we use to explain that two ratios are equal or equivalent. They are presented in the form: a/b = c/d. The division operator is sometimes removed or replaced with the symbol (:). Proportions are often given with unknown values. These unknown or missing values are easy to calculate by working off of the other three values that you are given. The unknown value would just need to satisfy the equivalence of proportions. They each serve their own based on what measures you working with and the nature of the data that you are exploring. Ratios are often given to explain unit rates and a wide variety of measures. Proportions are often used to compare the overall value of these unit rates and measures. Both of these have a wide array of applications, but you will use both any time you go grocery shopping.