Matrices Worksheets
When we are trying to understand more about a situation or scenario it helps to collect data that we can observe or calculate in those circumstances. When the information that we collect gets a bit overwhelming it is helpful to find methods to organize the data. A matrix is one such method that is often used by statisticians, analysts, and scientists. It arranges data, normally in the form of numbers, into rows and columns. A matrix is usually referred to by a capital Roman letter such as A, B, or C. In the worksheets and lessons, you will find below we will show you the basics of what this math is really about. We will progress you toward linear algebra.
- Add, Subtract, and Multiply Matrices - These worksheets will show you the proper approaches to solve matrices undergoing basic operations.
- Determinants and Inverses of 2 x 2 Matrices - These two measures help us understand if a solution may be present.
- Finding the Inverse of a Matrix - This concept relates to the use of reciprocals within fractions.
- Linear Equations as a Matrix Equation - This becomes very helpful when solving systems.
- Multiplying a Vector by a Matrix - There is a general formula present here that will help you solve it.
- Multiply Matrices by Scalars to Produce New Matrices - This allows you to amplify matrices.
- Null, Identity and Inverse Matrices - We learn to classify and proceed with the use of several different matrices types.
- Unique Properties of Matrix Operations - You will learn the ins and outs here.
- Using Matrices to Represent Data - This is really what it is all about. It allows us to crunch and process huge amounts of data.
What are Matrices?
In mathematics, matrices are defined as the rectangular arrays of expressions, numbers, and symbols, organized in rows and columns. Commonly matrices are written within box brackets. The singular is termed a matrix.
Elements Within Them - The numbers or symbols written in a matrix are defined as matrix entry or matrix element. We identify each by the row and column in which it appears.
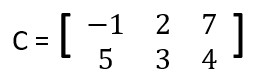
For instance, in matrix C (to the right) 2,1 is the matrix element in the second row and first column.
Dimensions - The dimensions of matrix give us the size of that particular matrix. The dimensions are a number of rows and number of columns of a matrix. The matrix C has two rows and three columns. We identify its dimensions as '2 x 3' and is read as 'two by three.'
Basic Types of Matrices - A matrix that has one row is known as the row vector, and those with one column are known as the column vector. Matrices having the same number of rows and columns are known as the square matrices. A matrix that has all elements as 1s in its main diagonal and the other elements are zeros is known as the identity matrix.
Basic Operations with Matrices - When we are working with two matrices that possess the same dimensions, you can add them by simply adding the numbers that are located in matching positions. The sum would then be in the form of a new matrix with the sums at those fixed positions. The same is true when you want to subtract two matrices. You would create a new matrix with the difference listed at the matching positions.
There are times when it makes sense to scale up a matric that we are working with. This is normally to make the math a little less complicated. When you multiply a matrix by a constant, we refer to that constant as a scalar. Which makes sense because by multiplying it by that constant we are scaling it up.
The use of matrices has become much more prevalent now that just about every computer in the world uses databases. A database is the core of fundamental concept of Matrix. Databases are used by businesses to track large amounts of data that is near impossible to manipulate manually. If you have ever posted anything online, you have used a database. They use this data to make well placed decisions and also to store content. They can also be used to encode and decode data to make your online purchases and information more secure.
Matrices are a pinnacle of statistics and analytical forecasting of all types. Because they allow you to process a great deal of data in more compact fashion. Most analysts routinely use them to model trends and find sticking points within a business model. They can be used to find opportunities that may not be readily realized otherwise.
How Are Matrices Useful?
When we first come across the concept of a matrix it presents itself as a pretty abstract concept. Once we get a hang of the math involved and get comfortable to a point where processing matrix operations seamlessly, we begin to ask ourselves why we are even learning this. There are many different applications of this form of math in the science and technology industries. If you progress towards learning a STEM based science curriculum it will first present itself in the field of physics. They are used to plot the three-dimensional (x, y, and z) coordinates of objects. We can then track the path or trajectory of these objects using simple operations and locational data. This same tracking leads itself to computer graphic and modelling software that uses similar relative location data. Matrix based instructions are given to robots in the manufacturing process of cars to automatically construct vehicles. In advanced computer programming this type of data modeling is used to encode and encrypt messages and data packets to transmit and receive secure transmissions and messages. This type of data format is used by geologists to survey seismic activity in earthquake prone regions of the planet. In the business world matrices are used to develop business forecasts on sales and to better understand market conditions based on local and world events.