• Point Translating Step-by-step Lesson - Move a point 90 degrees counter clockwise. There is a lot of vocabulary here.
• Guided Lesson - Where is the translation and reflection?
• Guided Lesson Explanation - Most of these problems require you to act like a witness to a crime. Yeah, that's the guy right there!
• Practice Worksheet - Sorry, this is one of my bigger packs. It has 6 pages and really requires that much room.
• Matching Worksheet - What would the coordinates be if this happened to it?

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

We get a bit extreme with translating points all across the coordinate plane.

• Homework 1 - A rotation turns a figure around a fixed point. 90° is 1/4 of a full turn. The rotation will turn the point 1/4 of a full turn in the clockwise direction. It looks like the diagram below if we are rotating about the origin.
• Homework 2 - A reflection flips the figure over a line to create a mirror image. A rotation turns the figure around a point. A translation slides the figure to a different location.
• Homework 3 - A glide reflection is the composition of a translation followed by a reflection across a line parallel to the direction of the translation. The image of a point (x,y) reflected across the xaxis is (x, y).

Practice Worksheets

Some of these will take you a good bit of time to size up.

• Practice 1 - Graph the image of B (35, -7) after a rotation 180° counterclockwise around the origin.
• Practice 2 - Which image shows a reflection of this shape?
• Practice 3 - Graph the image of ABCD after the following glide reflection: Translation (x, y) -> (x+9, y). Reflection across the x-axis.

Math Skill Quizzes

We move shapes and points all over the graph again.

• Quiz 1 - This focuses on the use of glides.
• Quiz 2 - This quiz hones in on the rotation around the origin.
• Quiz 3 - A reflection focused quiz.

Things to Consider When Drawing Transformations

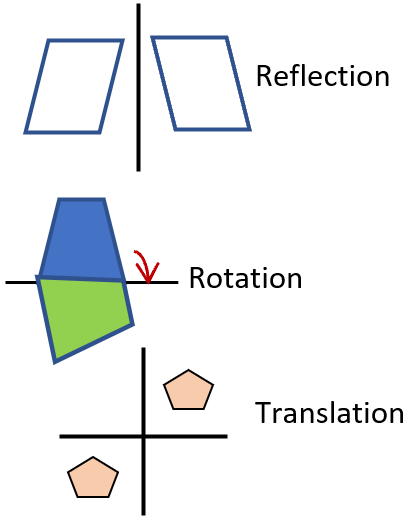
In geometry, transformed figures are those figures that have been moved from their original position on the coordinate system. Geometric transformations, in general, involve taking a preimage and transforming that later into some form of a new image. The definition of a transformation falls under two different categories. In a rigid transformation, the shape and size of the preimage don't change at all. In Non-Rigid Transformation, the size will change, but the preimage shape will remain the same.

Within the two categories that have been mentioned above, there are four main types of categories of transformations, out of which, three falls under the category of rigid transformation and one under non-rigid.

1. Rotation: When an object is rotated from its fixed point without any change in shape or size. When you are drawing these pay attention to angle and direction of the rotation. The direction is often stated in a clock directional.

2. Translation: Moving an object within the space without causing any change in the orientation, shape or size. This sliding of position will often be given in a unit number that correspond with the coordinate plane and directional within it.

3. Dilation: The contracting or expanding an object without changing its shape or orientation. This is often describe using a scale factor by which each linear measure of the figure is multiplied.

4. Reflection: This occurs when the object is flipped across a coordinate axis without any change in shape or size. In this case symmetry is maintained through the movement.