Rotations, Reflections, and Translations Worksheets
When an object moves across a coordinate plane, most likely a geometric shape, we call this change a transformation. These are the three most common transformations that you will find occurring. They all describe a different type of trajectory of movement and specify exactly how an object changes its direction, distance from the origin, and orientation. While most students see the identification of transformations as an exercise it truly is a math, specifically geometry, vocabulary building activity. When you are able to name these changes you are able to speak a new language that others can understand instantly. This series of worksheets and lessons will help you begin to immerse yourself in this new language.
Aligned Standard: High School Geometry - HSG-CO.A.4
- After A Translation Step-by-step Lesson - We rotate a figure and ask you what it would like after a simple counterclockwise rotation.
- Guided Lesson - Rotations, reflections, and clock directions, Oh my!
- Guided Lesson Explanation - I break rotations into 4 simple steps.
- Practice Worksheet - Shapes take up a lot of space that is why you'll see this one spread over 5 pages.
- Matching Worksheet - Match the figure diagrams to the translations.
- Identify Line Reflection 5 Pack - Are these reflections?
- Compositions and Glide Reflections Worksheet Five Pack - Start by identifying reflections and then move on to more involved problems.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
These problems always remind me of origami. It looks like a set of instructions.
- Homework 1 - Draw the line segment between the vertex and the point of rotation.
- Homework 2 - Which diagram shows abcde's reflection?
- Homework 3 - Which diagram shows ABCD rotated 20° counter clockwise about A?
Practice Worksheets
These problems require a higher level of thinking on the part of the kids.
- Practice 1 - Use a protractor to draw the angle of rotation.
- Practice 2 - A reflection flips the figure over a line to create a mirror image.
- Practice 3 - Which diagram shows a mirror reflection down?
Math Skill Quizzes
I did get a little carried away with the mirrored reflections. I will add a better spread of problems in a few weeks.
- Quiz 1 - Label each as a reflection, glide, or transformation.
- Quiz 2 - Is this a reflection?
- Quiz 3 - Use a compass to mark the rotated vertex point on the other side of the angle.
What Are Rotations, Reflections, and Translations of Geometric Shapes?
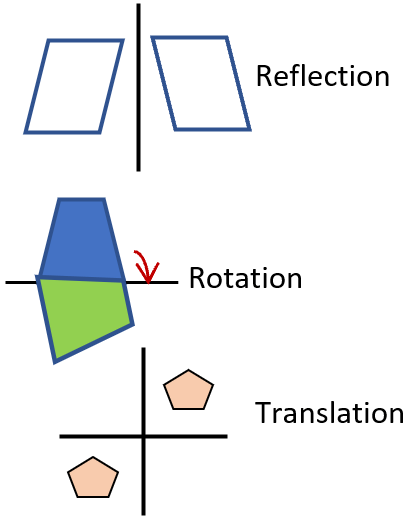
When a geometric shape is shifted or moved, we call that a transformation. Transformation is an important concept in geometry because it helps us describe this and communicate these movements to others. They are comprised of three sub-categories including translations, rotations, and reflections. To understand what these are, you can stand in front of the mirror and observe yourself when you move sideways and turn towards your side. What you observe in the mirror is exactly what rotations, translations, and reflections are in geometry.
Reflection - The most straightforward concept here is that of reflection. It is a common term that we come across very frequently in our everyday lives. So, what is a reflection in geometry? It is flipping of a point or an entire shape over a mirror line. The mirror line serves as a mirror on the graph. A shape and its reflected image are congruent, and both these are equidistant from the mirror line.
Rotation - Rotation is another term that we use almost every day in our lives. When tightening or loosening a screw you are rotating the screw at an axis of rotation. Similarly, in geometry, rotation is when we turn a shape around a fixed point, which serves as the axis of rotation. To rotate a shape on the graph, you will need the angle of rotation and the point of rotation.
Translation - Translation is simple. A shape and its translated image will have the same orientation and only the vertices will move sideways or upwards or downwards relative to the vertices of a shape. Both the original shape and its translated form are congruent. Each vertex covers an equal distance. This selection of worksheets and lessons teach students to identify and process these three common geometric transformations.