SSS and SAS Congruence Worksheets
When we are attempting to learn more about a geometric environment locating shapes that are congruent is normally our first step as they serve as landmarks to learn deeper about this environment. When it comes to proving congruence between triangles, we have five different methods for proving this. The two most commonly used theorems to achieve this are referred to as SSS (side-side-side) and SAS (side-angle-side). SSS tells us that if all the corresponding sides of the triangle are of equal length, then the triangles are congruent. Sometimes we do not know the measures of all the sides. For these circumstances we can use the SAS theorem. In that case if we know that two corresponding sides and the angle that forms between them are equal then the triangles are congruent. These worksheets and lessons will help you master the use and application of both of these valuable theorems. The focus pf the series is on proving triangle congruence through the use of side-side-side and side-angle-side theorems.
Aligned Standard: High School Geometry - HSG-SRT.B.5
- SAS Step-by-step Lesson - I focus on the other theorems more in the guided worksheet.
- Guided Lesson - You can find a great deal of help on this topic on the Internet that I never knew about.
- Guided Lesson Explanation - Creating these problems really opened my eyes as to how students can misread these types of questions.
- Practice Worksheet - I should have explained it better. Find the two triangles that can be proven to be congruent and identify the theorem used.
- Matching Worksheet - This one might confuse you at first, but I promise that you will see on national exams often.
- Proofs Involving Congruent Triangle Worksheet Five Pack - See if you can the commonality that I dropped in here.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
There is one homework for each theorem and the last one mixes both.
- Homework 1 - You can identify two triangles as being congruent when they are the same size and shape. SAS is another method for identifying congruent triangles.
- Homework 2 - Find the two triangles with two pairs of congruent sides and congruent included angles.
- Homework 3 - The three sides of ΔRTS are congruent to the three sides of ΔILU, so these triangles are congruent by the SSS Theorem.
Practice Worksheets
These are very quick ways to review proofs.
- Practice 1 - Which two triangles are congruent by the SAS Theorem? Complete the congruence statement.
- Practice 2 - Use the SSS Theorem here with this worksheet.
- Practice 3 - The SAS Theorem states that two triangles are congruent if and only if two sides and the included angle of one triangle are congruent to two sides and the included angle of the other triangle.
Math Skill Quizzes
It is all about finding the common sides on these problems.
- Quiz 1 - Using either SSS or SAS determine which triangles are congruent.
- Quiz 2 - To write the congruence statement, match the corresponding vertices. Since the side opposite R corresponding to the side opposite I, R corresponding to I.
- Quiz 3 - Use what you have learned to solve for what is presented.
What are the SSS and SAS Theorems?
We all are familiar with a three-sided polygon with three straight sides and three angles known as a triangle. How do you know if two of them are exactly alike? When geometric figures share the same shape and size, we describe the structures as being congruent. Two triangles are said to be congruent if they have the same angles and the same three sides. But in most cases, we aren't given all the three angles and sides of the triangle. To determine the congruence of triangles, three out of six (angles and sides) are a sufficient amount of information.
We have five ways to determine the congruence of a pair of triangles. They are described by the portions of the figures that are matching and them come under some great acronyms including: SSS (Side, Side, Side), - SAS (Side, Angle, Side), - ASA (Angle, Side, Angle), - AAS (Angle, Angle, Side), - and HL (Hypotenuse, Leg). Each of these proofs are substantial steps for understanding geometric environments, but for the purposes of this page we will focus on the SSS and SAS theorems.
SSS: SSS stands for 'side, side, side.' It implies that if two triangles have all three sides the same then they are congruent, and all the interior angles would also be the same. To determine the angles of the SSS triangle we would apply the Law of cosines to find out one of the angles. Then again, we apply the same law of cosine to calculate the second angle. Finally, we use the known angles to add them to 180 degrees to calculate the last angle.
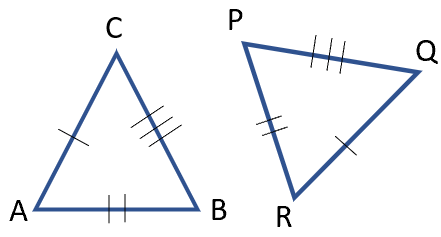
In the above figure, if BC = PQ, AC = QR, AB = PR, then the triangle ABC is congruent to triangle PQR. The dashes that are present on the triangles display those sides that are equal in length. Hence proving that the triangles are congruent if three sides of one triangle are equal to the three sides of another triangle.
SAS stands for 'side, angle, side.' It means that two triangles have two sides and one included angle between them are exactly the same. Not that this angle must be present between that two shared sides. To prove congruence by using SAS we apply the Law of cosines to find out one of the unknown sides. Then we apply the law of sine to calculate the smaller of the two angles. Finally, we use the known angles to add them to 180 degrees to calculate the last angle.
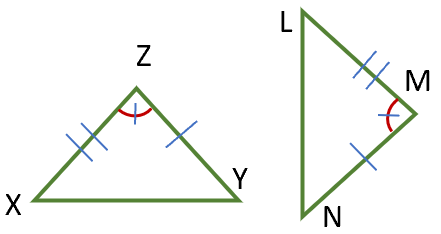
In the figure above, if YZ = MN, XZ = LM, and angle Z = angle M, then triangle XYZ is congruent to triangle LMN. Not that the lines and angles with lines through them indicate the same length or angle. Hence, we have proved that the triangles are congruent if the two corresponding sides and the included angle between those sides are equal.