Plotting Rational Numbers on a Number Line Worksheets
When students first come across negative values, they really get a bit confused. How could you have anything that takes away something that you do not have? Since they are not paying bills and understand the concept of debt, this is something that is still very abstract to them. A great way to begin to help explain the concept to them is using a number line. They are great for seeing where everything is in the general sense of things. I always present it like a visual of a race to the finish line. You can even use references to fables that they grew up in. The further to the right you go, the further you are in the race. In this selection of lessons and worksheets students will draw these values on a number line and get the idea of a negative value and complete change in value worksheets and lessons.
Aligned Standard: Grade 6 Numbers - 6.NS.C.6a
- Opposite of 5 Step-by-step Lesson- We use a numbers line to explain the negative value of 5.
- Guided Lesson - Explore how parentheses affect negative values and find more opposites.
- Guided Lesson Explanation - When you doubt, rely on the numbers line to think your way out of it.
- Practice Worksheet - I like the way this one came out. If you forget the concepts you can move to the next problem and be reminded yourself.
- Matching Worksheet - What number are they talking about? You decide.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
I think you will find the progression of each sheet to work well for you here.
- Homework 1 - On a number line, opposite integers are the same distance from 0, but in opposite directions.
- Homework 2 - Complete the number line below. Find the missing number.
- Homework 3 - What is the end value of: -(-2)?
Practice Worksheets
Each sheet seems to follow a common theme I have going on here.
- Practice 1 - When we open the bracket we get (- , -). Two negative cancel one another out and leave us positive.
- Practice 2 - What is the end value of: -(+25)?
- Practice 3 - If the missing value is smaller than 0, then subtract 1 from the next value. If the integer is greater than 0, then add 1 to the previous value to the missing part.
Math Skill Quizzes
I'm still stumped when students reach this level and don't understand the opposite of a rationale number.
- Quiz 1 - What is the opposite of 15?
- Quiz 2 - Complete the number line.
- Quiz 3 - All the thoughts in one worksheet.
How to Display a Rational Number as a Point on Number Line
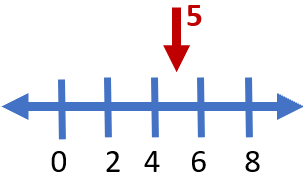
There are a lot of different types of numbers in mathematics, such as whole, integers, prime, natural, rational, and irrational. Rational numbers are those numbers that can be written in the form of fractions and both numerators and denominators are integers. These numbers can be easily displayed on the number line. A number line is a straight line that defines equal intervals or segments along the length of it. In a way they provide us with straight visual of where one value is compared to another. The segments increase in value from the left to the right. They are in fixed unit value from each segment. Take a look at the number line below the segments are broken into units of 2. The plot below shows where a position of 5 would be.
There are two types of rational numbers that are in fractional form; proper and improper fractions. Improper fractions are values where the numerator is larger than the denominator. When plotting rational numbers on a number line, you need to check whether a fraction is proper or improper. Proper fractions are easy to plot. I encourage you to change any improper fraction into mixed number form. Let’s take a look at how to plot the improper fraction 7/3 and the proper fraction 1 2/3 on the number line below.
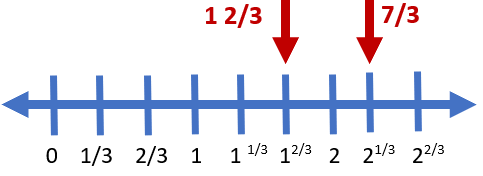
We can see the plot of 1 2/3 it is a visual segment on the number line. When you have to plot an improper fraction on the number line, you have to convert the improper fraction into a mixed number in the form of Quotient (remainder/dividend). The improper fraction 7/3 can be rewritten as 2 1/3. We can now easily place that on the number line, just like the other value. Check the number line above for the location of these points. When plotting, you need to remember that these fractions will always lie between Quotient and Quotient +1. The fraction part of the mixed number can then be marked just like a proper fraction, but it will not lie between 0 and 1.
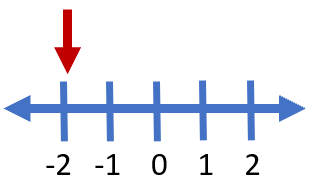
What about plotting negative numbers? The great thing about a number line is that it works in fixed intervals and can go in either direction (positive or negative). If the interval is 1, for instance, it could move to the right or left of the 0 point to create either negative (left) or positive (right) integers. How would you plot -2 on a number line that is set in intervals of 1? We can easily put this together, look below to see this plotted out for you.