Lines of Symmetry Worksheets
When we are working with various geometric figures, we can describe shapes that display equal sides as symmetry. A line of symmetry is a line that we can draw to cut a shape into exactly in half. This means that both sides of the line are exact match and mirror image of one another. In geometry we term these lines reflections for just that same reason. Understanding this property exists in a shape helps us understand the concept of balance and overload. As students begin to work at identify these properties in shapes, they will first see it as a very abstract concept. We encourage teachers to provide as many hands-on experiences as possible for them to become comfortable with identifying this balance and uniformity in shapes. This worksheet and lesson series will help students learn to identify lines of symmetry between several geometric figures.
Aligned Standard: Grade 4 Geometry - 4.G.3
- Step-by-Step Lesson- We tackle this concept head on. I always tell people, if it can fold on top evenly, it's asymmetrical.
- Guided Lesson - We again ask you if a drawn line shows symmetry, but we also have you draw your own lines.
- Guided Lesson Explanation - The answer keys are tricky when you have kids drawing their own lines. There are a lot of correct answers; I guess there are many wrong answers, too.
- Practice Worksheet - This is in a "bubble" this-and-that testing format. That is usually how you will see these types of questions.
- Matching Worksheet - Match shapes to a slice of their symmetrical ends. I never saw this before, just thought it was a fun way to do it.
- Transformation - Worksheet Five Pack - We look at the orientation of these objects and where they are caught at.Left to right or top to bottom?
- Read the Lines Worksheet Five Pack - Once again, left, right, top, or bottom. Where can you find that matching side?
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
I tried to cover this concept from every angle that I could; isn't that ironic?
- Matching Sides HW 1 - For it to appear we would have to draw the other half. Draw the other half to match.
- Drawing Lines HW 2 - How many lines of balance does each figure have?
- Defined Harmony HW 3 - This is when one shape becomes exactly like another if you flip, slide or turn it.
Practice Worksheets
You will decide not only how many lines of symmetry there are, but if you can qualify pre-drawn lines.
- Practice 1 - The lines are pre-drawn to provide you with guidelines. See how you make out with these.
- Practice 2 - Does the dashed display a line symmetry? Write yes or no. For extra credit explain why.
- Practice 3 - Draw the lines on all of these shapes to display a level of balance.
Math Skill Quizzes
These are some of the most interesting quizzes that I have ever created.
- Counting Quiz 1 - How many lines of symmetry does each figure have? These are some pretty cool figures to work with.
- Reflections Quiz 2 - Draw the other half to match. This quiz is asking you what is missing.
- Defined Quiz 3 - Are the lines correct? Some are and then again, some are not.
How to Identify Lines of Symmetry in Two-Dimensional Figures
A line of symmetry is a hypothetical or virtual line that divides a figure into two identical patterns or shapes. This is a visual skill that not all students will pick up right away. It is always a good idea to practice the things that you struggle with. We will explore a common technique to find these lines and explore common geometric shapes and what they exhibit.
The Folding Test - One of the most common ways of finding the line of symmetry is through a folding test. When a shape is folded, and it sits perfectly on top, i.e., matching all edges, then the fold line is called the line of symmetry. In affect one side of the figure is an exact mirror image of the other side.
The Basics - Take a look at the diamond shape below. What is interesting about a diamond (rhombus) shape is that all the sides are equal length. See if you find how many lines of coordination exist in this figure.

There are two different ways you fold a diamond to be an exact mirror image of the other. When you make these folds, everything sits perfectly on top of one another. Note the lines of symmetry that are drawn on the figure below.

Working with Triangles - These three-sided figures can have more than one line of symmetry. They come in three different varieties and have either none or one or three lines of it.
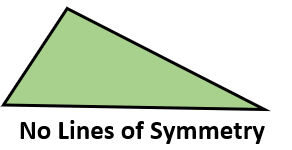
Scalene Triangles Have no equal sides or angles. Since nothing is the same on these triangles it is impossible to find a single line of symmetry. Therefore, there is no uniformity present.
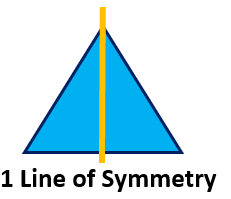
Isosceles Triangles These are figures where only two sides are equal, and therefore, it was only possible to make one line of symmetry.
Equilateral Triangles Are figures where all the sides and angles are equal, which makes it easier to make more than one line of symmetry. Being a three-sided shape where everything is equal, it possesses three lines of it.

Working with Quadrilaterals - Much like triangles these four-sided figures exhibit a wide variety of lines of symmetry. They can exhibit anywhere from zero to four lines of symmetry. Irregular shapes exhibit no lines of symmetry this is because there are no equal sides. Let's explore all the quadrilaterals that possess at least a pair of equal sides:
Kite - This is one of the less common shapes that you will come across. A kite is a quadrilateral that has two pair of equal length sides that are adjacent to one another. Because of the adjacent sides being equal you can only identify one line of symmetry in these figures.
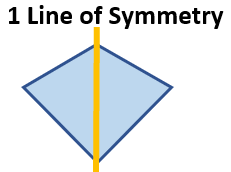
Rhombus - We saw this with the diamond shape at the start of this explanation, at the top. Rhombuses have side that all have an equal length. This results in two lines of symmetry (horizontal and vertical) being present.
Rectangles - The opposite side of these figures are equal, and all found at ninety-degree angles. Much like a rhombus this results in two lines of symmetry being present.

Squares - All the sides are equal and found at ninety-degree angles. As a result, there are four lines of symmetry in squares.

Working with Circles - This curved plane has all the pints on the curve an equal distance from the center point. As long as a line is drawn through that center, circles have an infinite number of lines of symmetry. They are shapes that are all about consistency and a state of equilibrium.
Why Is Identifying Symmetry Important?
Being able to identify a balanced system is helpful in many different applications. It as equally important as being able to identify asymmetry or imbalance found within a system. While many people think that this is a math skill while in fact it is life skill that will serve you well in many different walks of life. Symmetry is a foundational concept in geometry and helps us understand shapes, figures, and structures in many different technical aspects. There are times when you will want to shift a stable system to a less stable system. Maybe you need to redistribute supplies, maybe you need to bring more stability to another system by making another system less stable. Either way it all starts with being able to identify a system that is balanced and find signs of asymmetry within that system.