Rewriting Radical and Exponential Expressions Worksheets

This is one of those topics that will save you a ton of time. When ever you come across a radical expression you should try to simplify it by rewriting it using fractional exponents. In many situations this will save you bucket loads of time, not mention helping you avoid going down the rabbit hole of having to possibly work with irrational numbers. The next time you come across these types of expressions, just break it down into more digestible components in an easier to understand format. A series of worksheets and lessons that will show you how to rewrite both radical and exponential expressions.

Aligned Standard: HSN-RN.A.2

• Step-by-step Lesson- Start working on simplifying expressions that are found various forms.
• Guided Lesson - We show you how to breakdown products of these expressions in this batch just to uncomplicate things.
• Guided Lesson Explanation - These problems can take up quite a bit of room to work out.
• Practice Worksheet - You will work with all different aspects of converting between radical and exponential forms. What's with the shark?
• Matching Worksheet - Definitely give the kids some scrap paper to work with on this one.
• Simplify Radicals Five Pack- Take what you are given and make it simple to work with.
• Solving Exponential Equations (lacking a common base) Five Pack - The title pretty much says it all.
• Exponential Expressions and Equations Worksheet Five Pack - You are solving for x. They are mostly fractional exponents.
• Rationalize Denominators Worksheet Five Pack - You are also looking for conjugates of binomials and determining equivalent expressions.
• Evaluating Rational (Fractional) Exponent Worksheet Five Pack - I had to do a little refresher for myself before writing this one.

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

Use the properties of multiplication and roots to help you simplify the problems.

• Homework 1 - We need to break the square into smaller parts to simplify it.
• Homework 2 - To finish simplifying the expression, multiply by the whole to rationalize the denominator.
• Homework 3 - You can use the multiplication property of square roots.

Practice Worksheets

We removed clipart from the second and third versions to save you some ink.

• Practice 1 - Simplify the following expressions.
• Practice 2 - The multiplication property of square roots tells us that: √ab = √a × √b
• Practice 3 - A nice strategy is to group perfect square factors.

Math Skill Quizzes

Remind your students that the letter used as the unknown variable is negligible. We get a few question about that from time to time.

• Quiz 1 - Solve for the missing terms.
• Quiz 2 - Push the values to the proper side.
• Quiz 3 - You will be asked to find the end value of the expression.

How to Rewrite Radical to Exponential Expressions

Working with a radical expression can be cumbersome and at times lead to incomprehensible math. A great work around is to get rid of the radical portion of the expression altogether before you even start working with the expression itself. The best way to achieve this is often to rewrite that portion of the expression by using rational exponents. You can convert any radical using the fractional exponent form. The relationship between radical and rational exponents follows the form:

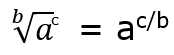
In the form that is display here the exponent the base number is raised to becomes the numerator in the conversion and the index of the radical becomes the denominator.

More on Simplifying Radical Expressions

You can also take a simple radical expression and break it into components by breaking it apart into a compilation of products within the radical. You can also do the same for radical quotients. These make them simplified and easier to work with in more advanced applications of math. This follows the models of:

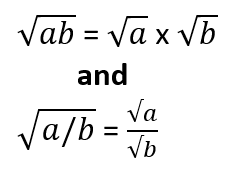
This makes working with radical values so much easier. Once you understand this, you have to truly grow an appreciation for working with radical expressions.

Converting Exponential to Radical Form

This is pretty much what we just learned, but in reverse. In my experience, you will use this less than the other way around, but it pretty commonly used when working with the geometry of circles. If we have a fractional exponent, we can convert the to a radical expression using the form:

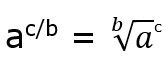
Using this form the numerator of the fraction becomes power that the base number is raised to and the denominator of the fraction becomes the root of the radical.