Parabola Worksheets
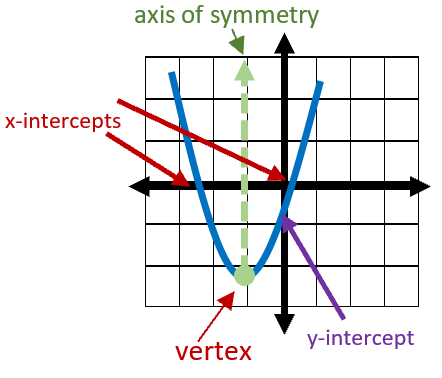
There four common features of a parabola that make each one unique. Let's discuss those key parts of this arched figure. The vertex is the lowest point on the graph and is characterized as the minimum value of the quadratic function. If the curve opens in downward position, this would be flipped, and it would be the highest point on the graph and the maximum value. The vertex is the turning point of the graph. The axis of symmetry outlines the trajectory of the parabola. The axis of symmetry is a vertical line drawn through the vertex. The y-intercept is the point at which the curve crosses the y-axis. There can only be one of these points when graphing a quadratic function. The x-intercepts are where the parabola crosses the x-axis and it will do so twice, so there are two points. All of these features are describe in the equation of a parabola. These worksheets and lessons help students learn to write and understand the equations of parabolas.
Aligned Standard: High School Geometry - HSG-GPE.A.2
- Parabola Equation Hunter Step-by-step Lesson - You are given a directrix and focus. We ask you for the equation.
- Guided Lesson - Three for you that are just like the lesson. A nice batch of practice.
- Guided Lesson Explanation - There are several ways to approach these. I like to calculate distance first and move from there.
- Practice Worksheet - Somewhat of a drill and kill way to explore this topic. It is effective for students.
- Matching Worksheet - Match the equation of the parabolas and their equations.
- Graphs of Parabolas 5 Pack - Just determine the point at which the graph cross the x-intercept.
- Write the Equation for the Parabola 5 Pack - Given the focus and directrix you need to determine the equation for the parabola.
- Graphs 5 Pack Part 2 - This is verbatim what the previous 5 pack was. I had many requests for more work on this, go figure!
- Classifying a Conic Section Worksheet Five Pack - Classify them based on their equation (Circles, Ellipses, or Hyperbolas).
- Find the Focus and Directrix Worksheet Five Pack - You will see a lot of these when you get working in this area.
- Find the Focus, Vertex and the Directrix Worksheet Five Pack - Pick each equation to pieces.
- Parabola Equation Worksheet Five Pack - More practice similar to what we see often on this concept.
- Matching Graphs and Equations Worksheet Five Pack - Which graph goes with which equation?
- Parabolas Worksheet Five Pack - It does look like I hit you twice with the directions.
- Equation Match Worksheet Five Pack - Another graph, equation match activity for you.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Find the equation when you are given the focus and directrix of a parabola.
- Homework 1 - The distance between (x0, y0) and the directrix, y=1 is y0-1
- Homework 2 - Simplify and bring all terms to one side.
- Homework 3 - This equation in (x0 , y0) is true for all other values on the parabola and hence we can rewrite with (x , y).
Practice Worksheets
The practice sheets add one slight new skill to the mix.
- Practice 1 - If the focus of a parabola is (4, -2) and the directrix is y=3, find the equation of parabola.
- Practice 2 - If the focus of a parabola is (1.5, -3) and the directrix is y=1, find the equation of parabola.
- Practice 3 - Equate the two distance expressions and square on both sides.
Math Skill Quizzes
The quizzes also look for the vertex and axis of parabolas.
- Quiz 1 - Find the vertex and axis of symmetry for each given parabola. Y= x2 - 8x + 7
- Quiz 2 - Find the Focus, Vertex and the directrix: x2 + 3x + 3y + 3 = 0
- Quiz 3 - Write standard equation for each of the parabola.
How to Find the Equation of a Parabola?
If you have ever noticed the shape of a satellite dish, then you have found a parabola. In mathematical terms, you get a parabola when you cut through a cone at a certain angle that is parallel to one of its sides. The simplest way to figure out the equation of this arch is by knowing the vertex, a point present on parabola itself.
Parabola Formula - What if we told you that you are familiar with the formula of a parabola? If you are familiar with a quadratic equation in the form of y= ax2 + bx + c, then you have found the standard formula of a parabola. But with some information about a parabola, then you can write its equation in vertex form, which looks like:
If the given parabola opens horizontally, then we use: x = a(x -h)2 + k
if the given parabola opens vertically, then we use: y = a(y -k)2 + h
Vertex - In both equations, coordinates (h, k) denotes vertex of the parabola, which is the point where the axis of symmetry intersects the line of a parabola. To break it down for you, if you fold a parabola from the middle in equal halves, the vertex will be the peak of the structure.
Determining the Equation - When you are asked to find the equation of parabola, you will be given enough information to find out the vertex or any other point on it.
Once you have enough information, you can calculate the equation in three steps.
1. Determine whether the arch is vertical or horizontal - First, decide the form of the vertex equation that you will use. If the curve opens horizontally (which means the open side of parabola faces up or down) then you will apply this equation:
x = a(y -k)2 + h
and in case the curve opens vertically (which means the open side faces left or right), then you will apply this equation:
y = a(x -h)2 + k
Assuming the parabola opens vertically, we will substitute the values in the second equation.
2. Substitute the values in vertex equation - Substitute the vertex coordinates (h, k) in the equation. Supposing the vertex lies at (1, 2), we will substitute h = 1 and k = 2.
y = a(x – 1)2 + 2
3. Using another point to find the value of 'a.' - Finally, you have to calculate the value of a. to do this, we pick any point (x ,y) other than vertex on the parabola, and substitute it in the equation.
Assuming the value of the point (x, y) as (3,5). So, we will substitute x = 3 and y = 5
Solving for 'a.' - y = a(x-1)2 + 2, 5 = a(3-1)2 + 2, 5 = a(2)2 + 2, 5 = a(4) +2 , 5 – 2 = a(4), 3 = a(4), a = 3/4 now, that you know the value of 'a', substitute it in your equation.
y = (3/4) (x -1)2 +2, is the equation of parabola with (1,2) vertex and having the point (3,5).