Measures of Arc Length Worksheets
An arc is just part of the circumference of a circle or other type of curve. When it comes to geometry there are number of unique features that we can use to learn more about the measures of arcs. There are three measures that are of particular interest on this subject. The radius is a line that touches any point of the circle and the exact center of that circle. The arc length is just the distance covered by that arc. The arc measure is the angle formed by extending radii out to the start and end of the arc. The length of an arc is equal to the circumference of the circle multiplied by the fraction of the circle that is represented by arc's length. These worksheets and lessons help students learn how to determine and predict the measure of arcs.
Aligned Standard: High School Geometry - HSG-C.B.5
- Colorful Arcs Step-by-step Lesson - Time to go all Pi and what not! We introduce you to using the formula that applies.
- Guided Lesson - These were tons of fun to put together. You will learn how to find these measures.
- Guided Lesson Explanation - Time to break down these explanations for you.
- Practice Worksheet - The simple measure of a radius can give you a lot of information.
- Matching Worksheet -Find the measures based on your stupendous knowledge of circles.
- Arc Length and Radian Measure Worksheet Five Pack- It's mostly all about radians to degrees.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Find the length of various arcs in many different exercises.
- Homework 1 - Where l is the arc length, C is the circumference, and m is the measure of the arc in degrees.
- Homework 2 - This one is pitched at a 30 degree angle. We give you a completed problem to work with, in case you forgot the basic procedure.
- Homework 3 - Once you have the circumference just pop it into the equation.
Practice Worksheets
Knowing how to properly apply the arc formula is easier said than done for most students.
- Practice 1 - The radius of a circle is 10 inches. What is the length of a 180 degrees arc?
- Practice 2 - Start with finding the circumference. We are looking to find the measures of blue sections.
- Practice 3 - The formula for the length of an arc is l = m/360 degrees x c.
Math Skill Quizzes
We master moving between radians and degrees. As you practice this skill, it gets easier.
- Quiz 1 - Convert π /8 radians to degrees. Then convert it back again.
- Quiz 2 - Convert 220° to radian measure. We also go back and look at the other skill as well.
- Quiz 3 - This is all in one. A nice big quiz. Six questions will keep you busy for a while.
How Do You Find the Measurements of Arcs?
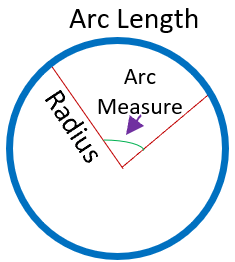
Circles are round figures that go 360 degrees all the way around. They are just a spate of points that are all an equidistance from the center. There are lots of terms related to the circle and one such term is called an arc. A segment of the circle around its circumference is known as the arc and its span along the arc is known as arc length.
An angle formed in the middle of the circle by the arc is known as the arc measure. Angles have two units of measures. The first unit is degrees, and degrees of angles represent the same fraction of the circle as its corresponding arc. For example, if you say 1/4th of the circle, the angle will be 90 degrees. So, the arc of a 90-degree circle will represent 14th of the circle. The second unit is known as radian. By following two rules, we can convert radians into degrees. Remember that a full circle is 360 degrees or 2π radians. A single radian is equal to 180 degrees. This will be helpful for you to remember as you work a great deal more with circles.
For conversion of radian into degrees, we multiply the radian measure by 180/π.
For the conversion of degrees into radians, we multiply the degree measure by π/180.
Let's say we need to find the radian measure of 70 degrees. You would just multiply 70 by π/180 = 1.22 radian.
How Does This Measure Apply to Real Life?
When we start working with circles it is difficult to see how this applies to your everyday life. You would be surprised by the sheer volume of application that this skill actual has. Just about any situation where you have a fixed object that travels in a circular pattern around where it is attached can be modelled in this manner. Think about a swing set. We all love to swing! Have you ever wanted to figure out how far you are actually travelling on that swing? Guess what formula can help you figure that out? What about situations where you are hurling an object? If you were to hurl a shot put as far as you possibly can, wouldn't it a great idea to know where you should release that object to maximize the distance that it travels? Photographers are experts on circle geometry since their lens are entirely based on this principal. They quickly learn that the quality of their images relates to the diameter of their lens and the focal length. Ship navigation is entirely dependent on this type of math as well. Have you ever seen a sonar output? Give it a quick Internet search. You will see that they look just like the diagrams that you see on the worksheets above.