Angle Bisector Worksheets
An angle bisector is formed when a line or a ray splits an angle into two congruent angles. The angle bisector theorem states that if a point is on an angle bisector, it is an equal distance from the side of the angles. Bisectors can help us learn a great deal of detail about geometric figures that are located within a coordinate plane. This piece of information often helps us form the foundation for geometric proofs. In this selection of worksheets and lessons we will work on how to first identify angle bisectors. We will then learn to draw these by hand and apply their use to supplemental geometric proofs.
Aligned Standard: High School Geometry - HSG-CO.D.12
- Bisect Lines Step-by-step Lesson - We show you how to use the compass to bisect a line like a pro.
- Guided Lesson - Angles and lines that you need to bisect with the help of your trusty compass again.
- Guided Lesson Explanation - All explanations are based on the use of a compass. This is standard tool that you need to master.
- Practice Worksheet - Time to sharpen your pencil for this one, it's going to be fun.
- Matching Worksheet - Yeah, I'm pretty sure I made this one just a bit too easy for you.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
It's all about drawing the sector of lines.
- Homework 1 - Using a straightedge, draw a line between the points where the arcs intersect.
- Homework 2 - Time to break out your compass. Place the compass's sharp point on the angle's vertex F.
- Homework 3 - This will create O point. Draw a line between the two points created by the O.
Practice Worksheets
Students should have this entirely mastered by the end of this series.
- Practice 1 - Bisect line segment MN.
- Practice 2 - Place the compass 1/2 to 2/3 of the line length.
- Practice 3 - Draw an arch below and above the line. Don’t change the compass width and place the compass on the other point. Draw an opposite arc.
Math Skill Quizzes
A mix of bisecting angles and lines.
- Quiz 1 - Adjust the compass to cover about half of a line.
- Quiz 2 - Place the compass on one point where the arc crosses a leg. Draw an arc that is on the interior of the angle.
- Quiz 3 - Grab a ruler and draw a line from the vertex of the angle to the point where the arcs meet.
How to Make Bisectors of Angles and Lines
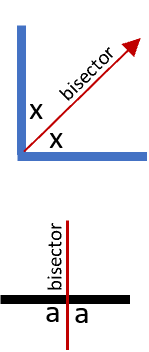
An angle bisector split an angle into two congruent angles. The same holds true with line segments. A line segment bisector will split a line segment into two equal and congruent parts. The Angle-Bisector theorem tells us that if a ray bisects an angle of a triangle, it divides the opposite side into proportional sides. We will now explore how to actually draw these on paper.
Steps to Bisect a Line Segment
1. Put the compass on point A and stretch the compass more than half to point B.
2. Draw an arc above the line segment AB and an arc below line segment AB.
3. Place the compass on point B with the same span, and draw arcs above and below the line segment AB. The two sets of arcs should intersect at two locations.
4. Draw a straight line connecting the two points of intersection, which should bisect the line segment AB at point C. This selection of lessons and worksheets help students learn how to bisect both angles and lines.
Steps to Bisect an Angle
1. Put the compass on the vertex of the angle, i.e., point B.
2. Stretch the compass to the length within the span of angle.
3. Draw an arc that crosses the two sides of the rays of the given angle. With that, you get two intersection points with sides of the given angle.
4. Put the compass on any of one of these intersection points on the sides. If required, stretch the compass to a length that draws an arc into the interior of the angle. Stay well between the sides of the angle and swing an arc in this interior.
5. Put the compass with the same span on the other intersection point on the side of the angle and draw a similar arc. The two small arcs should be within the interior of the given angle and intersect each other.
6. Connect point B (vertex of angle) to the intersection point of two small arcs.