Classify Two-dimensional Figures Worksheets
At this level we are focused on helping students learn how to delineate between the various three-sided (triangles) and four sided (quadrilaterals) figures. We start by looking at all the sides from triangles to octagons (8 sides). Once they have a handle on that, we move to looking at the properties of the sides and internal angles that are created by the sides to help students best understand classify all these different figures. There is some vocabulary that they will need to become familiar with, if you need a refresher look at the bottom of this page. These worksheets and lessons were put together to help students learn to quickly identify these 2D figures which they will get better at with consistent practice.
Aligned Standard: Grade 5 Geometry - 5.G.4
- Properties of Quadrilaterals Step-by-step Lesson- Tell us all the properties that you know for each shape.
- Guided Lesson - We ask you to name a specific set of quadrilaterals and see if we can prompt you in number two.
- Guided Lesson Explanation - There are a number of ways to answer these problems. Some people worry about sides, corners about corners.
- Practice Worksheet - Name each two dimensional figure that we throw at you.
- Identify Quadrilaterals Five Pack - You may have to draw a few too.
- Building Quadrilaterals Five Pack- We want fixed unit shapes. You might want to use a pencil with a good eraser for this one..
- Matching Worksheet - A nice mixture of problem types for you here.
- The Quadrilateral Family Worksheet Five Pack - Word problems that lead you towards naming a quadrilateral of some kind.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Make sure that you pay attention to the measure. They are there for a reason.
- Homework 1 - A 4-sided flat shape with straight sides that has a pair of opposite sides parallel.
- Homework 2 - Identify the shape.
- Homework 3 - It has 10 points and 10 equal sides.
Practice Worksheets
Some more shape reminders here. A lot of teachers tell me that they will give students the answers to these and ask them what the question is.
- Practice 1 - Identify and/or draw the Quadrilateral indicated.
- Practice 2 - There will be more than four sides here.
- Practice 3 - The sides that are parallel are called "bases". The other sides are "legs" (which may or may not be parallel).
Math Skill Quizzes
I totally got carried away with my true/false questions here.
- Quiz 1 - Identify the statements (true/false). "The opposite sides of parallelogram are equal and parallel to each other."
- Quiz 2 - The diagonals of parallelogram are equal in length.
- Quiz 3 - The diagonals of square are parallel to the base.
How to Classify Two-Dimensional Figures
Two-dimensional figures or shapes only have two measures of length (height and width) associated with them. There are several different properties that we can they are related to the sides or angles of the figure. When it comes to edges, we first classify them by the number of sides that they possess. We use a Greek prefix to name shapes based on their shape 3 edges = tri- (triangle), 4 edges = quad- (quadrilateral: square, rectangle, rhombus), 5 edges = penta- (pentagon), 6 edges = hex- (hexagon), 7 edges = hepta- (heptagon), 8 edges = octa- (octagon).
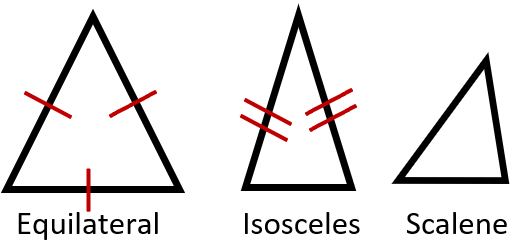
There are a great number of different types of triangles and quadrilateral. These are the figures that we work with the most often in geometry and architecture, so it is important to understand how to classify these figures. After we consider the number of sides, we focus our attention to properties of these lines and the angles that they create. When looking at the lines we try to determine if they are parallel meaning are always the same distance from one another and will never touch. We look to see if the edges form right angles and as a result have perpendicular sides. We also compare edges and see if they are congruent meaning that they are equal in every way. When it comes to angles were are looking at the types of angles (acute, obtuse, right) that exist in the figure and if there are any congruent angles in the structure. The angles that are present in triangles help us determine the classification. All the angles can be equal (equilateral), two sides (isosceles) can be the same, and no sides (scalene) can equal.
The prefix portion of the name of a shape indicates the number of sides of the figure. For example, a triangle has three edges, and a quadrilateral has four edges. Quadrilaterals take on many different names based on the angles and lines structure of the figure. Squares are a dead giveaway because they contain four right angles, and all their sides are equal. That differs from a rectangle that has two pairs of sides with equal length. Students will often confuse a rhombus with a trapezoid. A rhombus as two pairs of parallels and a trapezoid has only one pair of parallels. This will become much more common place for you as you gain experience working with these shapes. Here is a quick look at the basic classification of triangles and quadrilaterals in diagram form:
Triangles
Equilaterals have all equal sides. With isosceles two of these are two congruent. Scalene have no equal edges. The red lines below display the equal sides that are present.
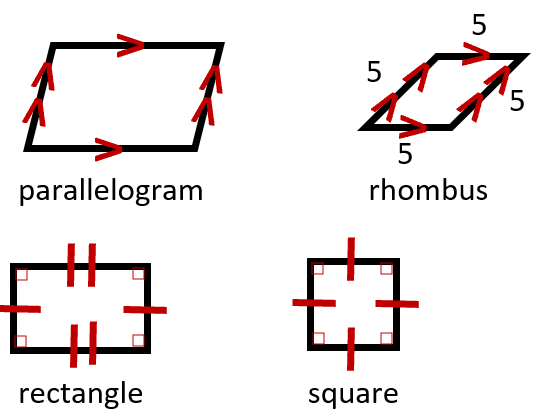
Quadrilaterals
A parallelogram is a figure where the pairs of their opposite are parallel. As a result, their opposite sides and angles are congruent. There adjacent angles are supplementary meaning that they add up to 180 degrees. When all the sides of a parallelogram are equal, we call this shape a rhombus. The commonly known shapes are rectangles which is a parallelogram with four right angle and squares that are rhombuses with all right angles and all equal sides. In this section we also take notice of trapezoids that are quadrilateral with only one pair of parallel sides.