Subtraction with Borrowing and Regrouping Worksheets
Once students have worked with base ten place values and understand that each successive digit in a number from right to left is ten times greater, they are ready to work with borrowing and regrouping in subtraction operations. We will use this strategy often when we are finding the difference between multidigit values. It could occur at any place value. When you come across a minuend that has less value then the subtrahend, you can also borrow from the place value above it. This adds a ten to the number that was lacking value. That is the process of regrouping. Remember that it also results in the value that you borrowed the tens from in being worth one less. I often find that students forget about this and that is where most of their difficulty is found. These worksheets and lessons teach students about the process involved in reordering (borrowing from higher places and regrouping lower places) subtraction problems.
Aligned Standard: Related to 2.NBT.B.7
- Caveman Lesson- We start to maintain the concept of subtracting right to left, but also look ahead.
- Guided Lesson - We chose problems that cover all places of borrowing. Lots of regrouping on problem 3.
- Guided Lesson Explanation - Only the third problem requires a long discussion.
- 2-digit Subtraction with Borrowing - You will find some extra space to work around with.
- Triple Digit Subtraction with Regrouping - You can also teach students to bunch problems. We start off with a bit of a dozzy.
- Answer Keys - These are for all the unlocked materials above.
Two Digit Practice Sheets
We encourage students to always start with the grid and then slowly move to the open question forms.
- Double Digit (In Grid) - Solve the following double digit subtraction problems.
- Double Digit (Open) - When subtracting multi-digit numbers, we start subtracting at the right and move to the left.
- Double Digit (Patterned) - To make it large enough to be subtracted, we borrow a one from the tens place.
Triple Digit Worksheets
Triple digit work is the height of this standard.
- (In Grid) - Find the difference for the following subtraction problems.
- (Guided) - Rewrite all these digits and subtract.
- (Fully Patterned) - Let's add some space in this problem to see it properly.
4-Digit Practice
Note that this is above the related standard. We thought we would it for gifted students.
- (In Grid) 1 - The ones place is too small. We will borrow from the tens place.
- (In Grid) 2 - Subtract the remaining digits towards the end of the problem.
What is Borrowing and Regrouping in Subtraction?
We know what subtraction is, right? When we remove a certain number from a bigger number, this mathematical operation is referred to as subtraction. In reality, we are trying to understand the difference or how far off the two values actually are. When we take away a certain amount, the original amount becomes less, and the result or the answer we get is known as the difference. The sign for denoting subtraction is called a minus, '-. '
Now, let's suppose that you are at your house, playing a board game with a group of friends. Suddenly, another one of your friends walks in and is asking for joining the game. That confuses the entire group, and everyone is thinking of how to add the new friend into their game (group). The teams that were created were even and had the ideal number of players. This leaves the groups with one simple choice; to regroup. You can take two or three people from the teams and let the new friend 'borrow' members from the previous team so that the teams now created match evenly! In mathematics this type of thing also happens when we are subtracting multi-digit numbers. Similar to the example, math also uses regrouping. When we do not have a sufficient number to take away from the amount given, we regroup and borrow from one group to the other so that the operation can be completed. Even though regrouping is not required in every subtraction word problem, sometimes it is quite necessary to use and can mess up the entire calculation if skipped!
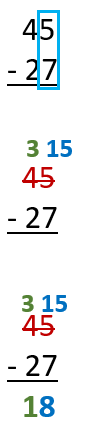
What if you were trying to find the difference between 45 and 27?
We first line the larger up in a vertical manner, placing the larger value (45) over the smaller values (27).
We then begin to subtract the values from the lowest place value towards the highest. In this case, the top number is smaller than the bottom number (5 - 7).
To make up for this, we will borrow from the next place value up (tens). As a result we subtract a tens value and make the tens place a 3. We then regroup that tens place and move it to the ones place. This elevates the original ones place value to 15.
Now we can subtract at the ones place (15 - 7 = 8). We write the 8 as the difference at the ones place and then we evaluate the tens place which is now (3 - 2 = 1). We write that in our tens place and we have our answer 45 - 27 = 18.