Four Digit Subtraction Worksheets
Learning how to subtract three-digit values really sets the foundation for all forms of large differences. This is because it covers all the skills that are required for you to be successful. Four-digit subtraction should not be a huge leap for students. It simply requires that they stay organized and keep their columns lined up. The biggest challenge I find that students have is keeping their digits clear when borrowing and regrouping. I encourage them to always write much smaller digits or use colors to keep this organized. Color the higher place one color and the lower place a different color. That little tip usually pays tremendous dividends. These worksheets and lessons help students learn how to find the difference between numbers that are composed of four digits.
Aligned Standard: Core Operations
- Getting Hooked Step-by-Step Lesson- It takes a few pages to explain this one.
- Guided Lesson - I like to space out the numbers within the integer well so students can spatial recognize it better.
- Guided Lesson Explanation - Three problems, three pages of explanation. They should have a solid grasp of the concept after this one.
- Practice Worksheet - I have to pat myself on the back for putting this one all together on one page.
- Matching Worksheet - Big digits make for big differences.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
No big frills here. Straight horizontal differences for you to practice with.
- Homework 1 - We subtract from right to left digit.
- Homework 2 - You will need to borrow several times here.
- Homework 3 - We cannot subtract a bigger number from a smaller number. You can, but you will learn that down the road.
Practice Worksheets
We keep it all together using the same rhythm and flow given off by the homework sheets.
- Practice 1 - A little less borrowing is found here.
- Practice 2 - Drop down the values to remove doubt.
- Practice 3 - Subtract the values vertically.
Math Skill Quizzes
These all follow the same standard as all the previous sheets. This is a popular quiz topic.
- Quiz 1 - If the bottom number is larger than the top value, you will need to borrow a ten.
- Quiz 2 - Borrowing is kind of like buying a pizza, when you don't have money.
- Quiz 3 - I suggest you plan how you will approach each problem, first.
How to Solve Four Digit Subtraction Problems
Just like any math operations if you follow a consistent plan and approach as to how you will solve them, you be successful, and it will eventually become easy for you. The basic approach to solving any multi-digit subtraction problem is to evaluate at the lowest place value, borrow (if needed), regroup (if needed), and then rinse and repeat at the next highest available place value. You continue on through this procedure until you run out of numbers to evaluate. Let's work through an example of carrying out this strategy by solving the difference between 5,481 and 3,569.
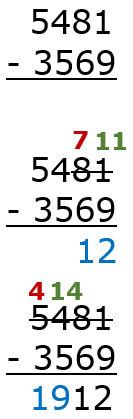
Step 1: Write the Problem Vertically - The first thing we need to do is position the minuend and subtrahend in an alignment that clearly allows us to visualize the place values.
Step 2: Evaluate the Lowest Place Value - The lowest place value, in this case is the ones place. The minuend is a 1 and the subtrahend is a 9. We cannot process this difference without creating a negative value. So, we must borrow from the higher place value (tens). We borrow a ten from the tens place (8). We then regroup that value to the ones place and create 11. We can now evaluate both the ones and tens place. This leaves us with 12.
Step 3: Evaluate the Next Highest Place Value - The next highest place value is the hundreds column. We run into the same type of issue here. The minuend is 4 and the subtrahend is 5. Once again we must borrow from the next highest place value which is the thousands. We drop the 5 (thousands place) to 4 and carry that thousands value to the hundreds column creating 14. We then can once again are allowed to evaluate both the hundreds and thousands column. This leaves us with 19. We have found our final difference at 1,912.
How do Computers Subtract Numbers?
The original purpose of the computer was to solve complex problems. However, what happens inside all this technology? You must know that computers understand problems in the form of binary numbers. Therefore, first, they convert both numbers into their binary equivalent. However, to subtract binary numbers, you need to learn 1's and 2's compliment. Let's solve the problem with an example.
You need to solve 7 - 4. Firstly, you will need to convert 7 and 4 into their binary equivalent, which is 0111 and 0100, respectively. Now, to subtract a binary number, we need to perform 1's compliment, which means we will have to switch the bits (i.e., 0 to 1 and vice versa) to 1011. The next step is to add 1 to the converted bits to make it 1011 + 1 which is 1100. Now, you can add this with the binary equivalent of 7, which is 0111 + 1100, and the answer is 10011. You can now neglect the leftmost 1 and the answer is 0011, whose decimal equivalent is 3.