Lattice Method of Multiplication Worksheets
In this section we share the lattice form of multiplication with you. This is a technique where you draw a series of boxes and diagonal. Hence the name, lattice. Around this lattice you fit your multiplier and multiplicand. You then write the product of each digit in the boxes separating the place values by the diagonal. When you find the sum of all the diagonals, they are equal to the overall product. This can be used for 2 and 3 digit products. It is all how you set it up. These worksheets and lessons show students an easier method to use for greater success when you are multiplying very large numbers.
Aligned Standard: 4.NBT.B.5
- Lattice Method Step-by-Step Lesson- We show you how to use this approach to simplify your products. It just might help a great deal.
- Guided Lesson - Two problems with a empty lattice matrices for you to use.
- Guided Lesson Explanation - I made a detailed visual key for these. I think it will make it easy for students to do by themselves.
- 2x1 Practice Sheet 1 - 10 problems spread over 2 pages.
- 2 x 1 Practice Worksheet 2- The second page with only two problems is purposeful. You can use these as DO NOW problems or review.
- Answer Keys - These are for all the unlocked materials above.
2 x 1 Practice Sheets
Just two more to give you even more practice.
- Practice 3 - When you are multiplying large numbers you can use the lattice method to simplify it for you.
- Practice 4 - The lattice uses boxes that break things into place values.
- Practice 5 - Since we have two 2-digit numbers we will need 4 boxes.
2 x 2 Homework and Practice Worksheets
We step it up to the next level 2 digit by 2 digit products.
- Homework 1 - Set the numbers we are multiplying across the top and side of the lattice we have created.
- Homework 2 - Multiply the numbers that meet in each box separate the products into place values using the diagonal line.
- Homework 3 - Add the numbers between the diagonals to get your answer.
3 x 2 Practice Sheets
This might be were the lattice method loses students. Just keep them organized and they shouldn't have any problems.
- Practice 1 - Place numbers involved across the top and side of the lattice.
- Practice 2 - Multiply the numbers that meet at each box. Separate the products place values (tens and ones) using the diagonal line.
- Practice 3 - Find the sum of the numbers that are under the same diagonal line.
What is the Lattice Method of Multiplication?
Do you find long multiplication, boring and tiring? Well, there's no doubt that sometimes long multiplication takes forever. The good news is mathematics has an alternate for almost every concept. There are many other ways you can multiply with two- or three-digit numbers without using the long multiplication method. One such method is the lattice method. You may also hear it referred to as Chinese multiplication.
The lattice method gives you an alternative way to multiply more than one digits. The method uses a grid with diagonally written numbers that make a crisscross pattern. Hence it is called a lattice method. If you look around you will find out many crisscrosses or lattice patterns in your daily life, such as your grandma's delicious blueberry pie. This can be very handy because it takes large values and breaks everything down into simple math facts.
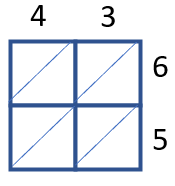
There are three basic steps to using this method are:
Step 1: Prepare Lattice - This requires you first to draw the lattice which is just four squares stacked in a two-by-two arrangement. You then place right faced diagonal slashes in each box. You will then place the two-digit values that are being multiplied on around the squares with the multiplier on top and the multiplicand on the right of the boxes. For the purposes of this exercise, we will work on find the product of 43 and 65 (43 x 65).
Step 2: Multiple the Digits - You will match up each of the digits that meet in each box in the rows and columns. As you will see in the image below. These pairs meet up 4 and 6, 4 and 5, 3 and 6, 3 and 5. Place the tens value of that product to the left of the diagonal slash and the ones place to the right of it.
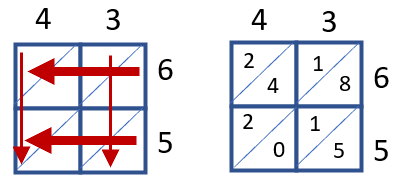
Step 3: Add’em Up - You will add each diagonal value within the grid. The best way to go about this is to extend the diagonal by ending the slash in each box. Starting in the bottom right we find the sum of all the digits found within the diagonals. We can see 5 by itself, in the bottom right, so the sum is 5. The next diagonal up has us add 0, 1, 8 (0 + 1 + 8 = 9)which is 9, so we write that digit in that place. The next diagonal has us find the sum of 2 + 4 + 1 = 7. The last diagonal is just 2. So our final product is 2,795.
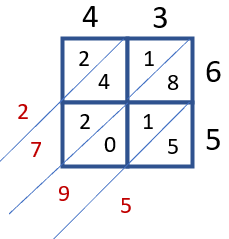
This method of multiplication has been around for ages, probably since the Middle Ages, or even before your parents were born into this world. This method helps students in improving their organizational skills; it breaks down the process of long multiplication into smaller steps. At first, it might seem like a complicated task, but you'll learn to do it with time.