Multiplication 3 by 3 Digit (In Grid) Worksheets
When students begin to work with 3-digit multiplication it is entirely about staying organized. These problems can get quite lengthy and require a humongous amount of paper. They simply are not confined enough to process these problems on a digital device. I remember when our department forced us to have students complete all work digitally. This was a complete disaster, I felt bad for the kids. They would setup the problem, get to the second-place value and have to scroll down which made them lose complete vision of the problem. That is where grids come in and change the game. The place values are perfectly set with these sheets. It would greatly benefit your students if you got them into the habit of creating their own grids and setting up problems vertically. These worksheets and lessons will help students learn how to multiply two values that are composed of three digits each with the backdrop of a grid.
Aligned Standard: 4.NBT.B.5
- Place Setting Step-by-Step Lesson- I work you through each number, just remember the place value of the bottom numbers.
- Guided Lesson - I put the zero in the second problem on purpose, it helps beginners.
- Guided Lesson Explanation - Three problems, three pages of answers.
- Matching Sheet - I left the commas out to make it slightly more difficult.
- Practice Worksheet - I didn't give space above the numbers, sorry I couldn't fit it.
- Triple Times Triple Digit Multiplication 5 Pack - Work you right through this pack to mastery of the skill.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
There are a great number of steps for these problems. Take it slow and stick with it.
- Homework 1 - First we multiply 9 by 896 . Then we multiply 6 by 896. Then we multiply 2 by 896.
- Homework 2 - You can use place value holder when ever you need it.
- Homework 3 - The tens place value is a single variable and the hundreds is a double variable.
Practice Worksheets
The grid really makes aligning the numbers a cinch.
- Practice 1 - You can use the double variable xx to represent a 00 holding the hundreds place.
- Practice 2 - You will need to extend a column over or even more.
- Practice 3 - Space your work out here.
Math Skill Quizzes
This is definitely a section that gets a lot of people fired up! Some people love the grid and others think that it makes kids lazy.
- Quiz 1 - Time to see what you know.
- Quiz 2 - A good mix of problems for you.
- Quiz 3 - These problems are slightly more difficult than the previous two.
How to Multiply 3 Digit by 3 Digit Numbers
Until this point students have stayed pretty organized when solving product-based problems. There was a little bit of leap going from single to double digit multiplication. Going from 2 digit to 3 digit multiplication is a much greater leap because it requires that stay extremely organized. You need to track a minimum of 3 place values and a maximum of 6. Which can get a bit more complicated. We encourage you to get in the habit of using the grid method that we played out for you here. This will allow you to track any and all movement as you form the product.
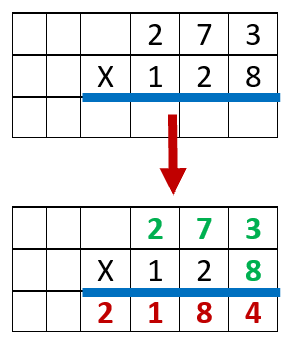
When you are processing these problems, there will be three product based steps, one for each place value. You will then finish off the problem by finding the sum of all the products. Here is a full example for you and we will track the steps along the way using the base problem: 273 x 128.
Step 1) Setup and Multiply Lowest Place Value - We created a grid and place our largest value (273) as the multiplicand (top value) and our lesser value (128) as our multiplier (lower value). We then multiply the ones place (8) of the multiplier by the entire multiplicand (273).
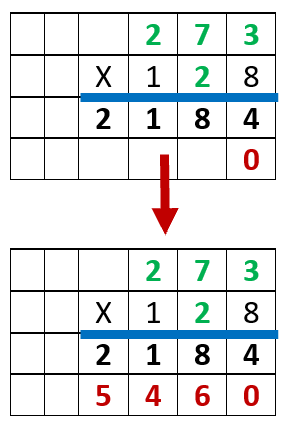
Step 2) Multiple Next Place Value - The entire time that are processing this problem we keep the previous product (2,184) in place, as a reminder, to be summed up at the end. We complete the product of the ones place of the multiplier, we will now move on to find the product of the tens place (20). We begin by adding a zero to final product since we are working with a tens place. We then proceed just like we did with the other place value.
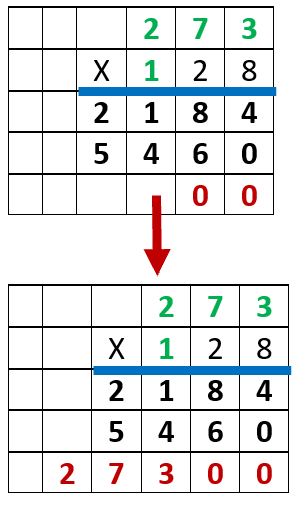
Step 3) Multiple Next Place Value - We finish this off by multiplying the hundreds place of our multiplier by the multiplicand. Again, because we are multiplying by a hundreds place we must place two zeroes to the back of our product.
Step 4) Find the End Sum - All we need to do to find this off is find the sum of all three of the products that we have determined. So, it would present as: 2,184 + 5,460 + 27,300 = 34,944.