Logarithmic Functions Worksheets
As we progress towards learning calculus, we need to have a better understanding of how manipulate exponential equations and expressions. Logarithm functions allow us to better exploit these types of mathematically statements. When we are modeling situations that have a great deal of amplification with math, they come in very handy. In this section we will explore this relationship and learn to model scenarios with both forms of notation. We will also learn how to determine the constraints of these types of functions to better understand their limits of use for our needs. As you explore more advanced forms of science, you will see the potential uses for this type of math. These worksheets will help students read and interpret logarithmic functions in a wide array of situations.
Aligned Standard: HSF-LE.A.4
- Simplification Step-by-Step Lesson- Combine and draw down from the variables that are present in this set.
- Guided Lesson - Simplify a log yet again, find the range of a statement, and write an equivalent statement.
- Guided Lesson Explanation - The second problem might be a bit of novice explanation, see if it is clear.
- Practice Worksheet - Make statements simple, find more ranges, and hunker down with more log statements.
- Matching Worksheet - I just realized that a and j are the same. I'll get a fix out soon.
- Answer Keys - These are for all the unlocked materials above.
- Practice Worksheet 2 - You will practice finding both the x and y intercepts and writing in exponential form.
- Homework Sheet - More work on the exponential form and you will determine the range.
- Quiz - We will assess what you understand about the three skills we have highlighted in this section.
What Are Logarithmic Functions?
Much before calculus, mathematicians used logarithmic functions to help them with complicated math problems. Like calculus, logarithmic functions helped mathematicians in converting multiplication problems into addition and subtraction problems. The substantial importance of logarithm functions lies in their ability to help us make sense of exponential equations. Anything that deals with a large or small scale of values can be helped by harness your understanding of this form of math. Even today, scientists and mathematicians have to encounter problems with large powers and complicated products. This is where logarithmic functions are invaluable. They are often used in calculus to determine the slope of certain functions which helps understand their constraints.
Definition of Logarithmic Function - In mathematics, a logarithmic function is defined as the inverse of the exponential function. Any exponential function can be easily expressed as the logarithmic function. Similarly, a logarithmic function can be expressed as an exponential form. The logarithmic function allows us to work with large numbers, especially those with large powers. A logarithmic function is expressed as:
For x > 0, a > 0, and a ≠ 1
y = logax if and only if x = ay
Then the function is shown as: f(x)= loga x
‘a’ is the base of the logarithmic function. This is usually read as the log of base a of x. Logarithmic function commonly has two types of bases, which are base e and base 10.
The logarithmic function that has base 10 is known as the common logarithmic function. It is denoted by log10 or is simply known as log.
f(x)= log10 x
The logarithmic function that has a base ‘e’ is termed as the natural logarithmic function. It is denoted by loge
f(x)= loge x
How is the Exponential and Logarithmic Form Related?
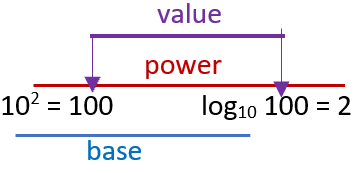
Until this point, we have focused on the use of exponential form. Which follows the comfortable form of math that we are accustomed to. This follows the skeleton form of: basepower = value. The logarithmic form of these types of equations are just a slight realignment. The follow the skeleton form of: logbase value = power. They are not too far off of one another. If you look at the diagram below, you clearly see how the two forms of notation are related. We take the exponential form of 100 and convert it to logarithm form. Note the placement of the base, power, and value.