Lines and Angles Worksheets
The foundation of geometry centers around understanding the measures of the length of lines and angle measures. The beauty of this subject is that there are a ton of different ways that both lines and angles are related especially when it comes to triangles. Based on the type of line or the nature of the geometric shapes that you are working with it is often easy to spot congruent angles and sides. This can often best be described by the orientation of the lines or sides of the shapes and how they connect or contact one another. These worksheets and lessons help students learn how to name angles and make sense of line relationships. The goal is to help students get set for higher levels of math like trigonometry.
Aligned Standard: HSG.CO.C.9
- Defining Measures Step by Step Lesson- We learn to spot corresponding, alternate exterior, and consecutive interior classifications.
- Calculating Measures through Relationships Guided Lesson - You are given an angle created by a transversal cutting two parallel lines. See how many more angles you can determine.
- Guided Lesson Explanation - We mostly explain the use of alternate exterior and supplementary values.
- Exterior Angles Worksheet 1 - This where geometry and algebra meet.
- Neat Names - Worksheet 2 - We post and name corresponding, alternative interior, alternate exterior, consecutive interior, and consecutive exterior.
- Identify the Angle Type - Working off a set of parallel lines cut by a transversal you will name all eight angles that are formed.
- Algebra and Angles - You will use algebra to determine the missing measures that are presented to you.
- Working with Measures 4-Pack - This pack of four sheets covers a wide area of angle based skills.
- Answer Keys - These are for all the unlocked materials above.
Angles Formed By Transversals Review
The angles that are formed by a transversal cutting across two parallel lines leads us to learning how to determine seven other measures, when only given one.
- Lesson - You will learn how to describe the relationship that exist between the angles list below. Also how to indicate what this relationship tells us mathematically.
- Review Sheet - We go over all the different forms of congruence and supplementary values that are created.
- Transversals Guided Lesson - Find the measures of all the missing angles below.
- Transversals Guided Lesson Explanation - You will see that this is just a rocket ship that takes off, once you can determine the value of a single measure.
Homework Sheets
Start by using exterior angles. Then determine the measure of unknown measures through algebra. Finish off by labeling them.
- Homework 1 - Find the value of x. Assume that all paired lines are parallel.
- Homework 2 - When the parallel lines (t and x) are cut by a transversal the angles formed in the same relative position, to each line, are considered corresponding.
- Homework 3 - Given that line m and n are parallel, tell whether each set are supplementary or congruent.
- Homework 4 - In the diagram below two parallel lines are cut by a transversal. Fill in the blanks with the value of x.
- Homework 5 - We will use algebra to find the missing value.
- Homework 6 - Match each angle pair with the correct name.
- Homework 7 - You will name the construct name that exists for each angle.
- Homework 8 - You will identify the relationship between each angle and then find the missing measures.
Practice Worksheets
This series of practice worksheets focus on understanding and using the measure of angles.
- Practice 1 - When each of the angles are outside of the parallel lines and on opposite sides they are referred to as alternate exterior.
- Practice 2 - Angles that are found on one side of the transversal and inside the parallel lines are referred to as consecutive interior.
- Practice 3 - z is an alternate exterior angle to the known angle measure (140°). Alternate exterior angles have equal values. The measure of ∠z is therefore140°.
- Practice 4 - You will use algebra to find the missing values and determine their measures.
- Practice 5 - Name the relationship that exists between the measures that are named here.
- Practice 6 - Analyze how each measure relates to the given value.
- Practice 7 - You might just be amazed at what you can tell by just knowing a single measure.
Math Skill Quizzes
Student define the relationships that they find from parallel lines that are cut by a transversal.
- Quiz 1 - x and the known angle (140°) are supplementary angles. This means that the sum of
- Quiz 2 - Give the name of the relationship for each set of angles.
- Quiz 3 - What is the value of x in each of these sets?
- Quiz 4 - We get back to using our good friend algebra to help us here.
- Quiz 5 - Given that line m and n are parallel, tell whether each set of angles are supplementary or congruent.
- Quiz 6 - We will apply all the skills that we have learned in this series to get after it.
- Quiz 7 - Work off of the single value to find all the measures.
Common Line and Angle Relationships
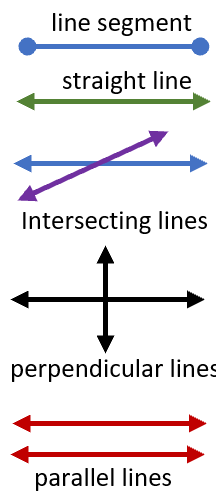
It is always good to understand the basic vocabulary you are going to run into when you are working with geometry. If you can read a description of these and then visualize them with a simple drawing, you are in good shape. For more in-depth descriptions check the lesson listed above.
A line segment has a start and an end point with a set length. Straight lines on the other hand, lack end points and have infinite lengths. There is some terminology that describe how two or more lines interact with one another. When lines cross each other in a plane they are termed to be intersecting. If a line intersects a series of other lines, it is called a transversal. If two lines meet at a right angle their relationship is described as perpendicular. If two lines are found on a plane and they never meet because they are the same distance apart, they are termed to be parallel. When two lines meet, they will often form angles. There are three classifications of angles based on their measure. If the measure is less than ninety degrees, it is called acute. If the measure is exactly ninety degrees, it is called a right angle. If that measure is between ninety and one-hundred and eighty degrees, it is called obtuse. There are also classifications given to pairs of angles that measure ninety degrees (supplementary) and one-hundred and eighty degrees (complementary).
What are Alternate Exterior and Interior Angles?
When two rays meet each other at an endpoint, an angle is formed. In other words, an angle is a distance between two rays. A transversal line, as the name implies, crosses or traverses through the two lines. In some cases, two other lines are parallel to each other, and a transversal line passes both the lines at the same angle. The two other lines don't necessarily have to be parallel for a transversal line to cross them. When a traversing line crosses through two parallel lines, some special properties of the angles are formed that are not likely to occur without the two parallel lines. Alternate Interior - We get alternate interior angles when a transversal crosses through the two lines. Angles present on the opposite sides of a transversal, and inside the two lines are alternate interior angles. An easier way to remember the alternate interior angle is that the pair of alternate interior angles form a z-pattern. Alternate Exterior - When a traversing line passes through the two lines, the pair of angles present on the outside of both lines and the opposite side of the third line is called as alternate exterior angles. Note that the pairs are present exteriorly of the line that passes through the two lines, and all the measures are also present exteriorly too.
What are Transversal Lines?
When two lines are an equal distance apart and never meet, we refer to them as parallel lines. They can literally point in any same sided direction, as long as they meet those two criteria. When a line crosses over both of these lines it is referred to as a transversal line. Each transversal will create eight new angles of it. If you can in fact find the measure of just one of those eight angles, using simple geometry, you can learn the measure of all eight angles. If you know one angle on the transversal, the angle directly opposite it, must combine with it to form a one-hundred-and-eighty-degree angle. If we remember back to the concept of vertical angles (they are equal), we now know how to find the other two remaining angle. Angles (corresponding) from matching corners are considered to be equal. We also know the alternate interior as well as alternate exterior measures are equivalent. The same also holds true for consecutive interior angles.