Triple Digit Division Worksheets
Usually there us a big leap for students who transition from single to double digit division. I do find that skill much harder to teaching than working with quotients that include triple digits. This is because they have already learned the concept, we are just throwing another place value at them. So it is much more manageable. I would always start this unit by reviewing the lower place values first and then just throw them in there and see how they handle a problem like this. A chest filled with worksheets and lessons that help students learn how to divide three-digit values by one-digit numbers.
Aligned Standard: 4.OA.B.4
- A Real Long One Step-by-Step Lesson- It still only takes one step to get it done.
- Guided Lesson - There are no remainders found here.
- Guided Lesson Explanation - Seven and nine make it more difficult than odd numbers.
- Matching Sheet - Match the quotients to their outcome.
- Practice Worksheet - The font is large and extended. The top one could be tricky.
- Matching Sheet - See if you could fit this all on one sheet.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
The horizontal format is used here. You will see an open parentheses to the right of the divisor to help children focus on the quotient. This works nicely.
- Homework 1 - Use the outline to help you shape the problem.
- Homework 2 - If there is a remainder, just give it a bit more time.
- Homework 3 - A fully worked out example is provided.
Practice Worksheets
Again, practice sheets only have five problems and a lot of space to work with.
- Practice 1 - These can actually be done mentally.
- Practice 2 - Smaller into larger values.
- Practice 3 - We use larger divisors now.
Math Skill Quizzes
Each quiz sticks with the horizontal and extra parentheses format to make these problems very manageable.
- Quiz 1 - Where would you start with these?
- Quiz 2 - The values will indicate that no remainders will be found.
- Quiz 3 - A lot of round numbers can be found here.
How to Divide a Triple-Digit Number by Single Digits

The division is a basic mathematical operation that is taught to create an idea of how to distribute something in several equal sectors. The come scenario that we share with students is splitting a pizza with friends. Normally during a division operation, a number that you have to split up is called a dividend and is kept on the left side of the division symbol (÷). And the number that signifies the number of groups the dividend will be broken into is called the divisor and is written on the right side of that same symbol. The answer, also called ‘quotient', comes at the top, and the remainder comes at the bottom. A remainder is a leftover part that can't be accommodated in the division if someone wants their answer to be a whole number.
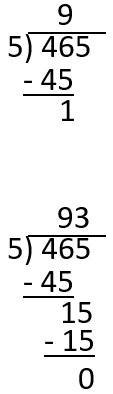
The step-by-step process of dividing a triple-digit number by a single-digit number is simple. First, we break the triple-digit number and consider it a digit at a time. Then we divide it digit by digit by the divisor and write the answer to every sub-division at the top, which makes the final value for quotient after the last digit is divided. If the last digit cannot be divided completely, giving a whole number as an answer, a remainder is written carrying the leftover value.
Take a look at this example and follow all the steps that we will take.
Example problem: 465 ÷ 5
Step 1) Working from the left, we see which value 5 can fit into. 5 is bigger than 4, so we will move to the next place and determine how many times 5 goes into 46. It will go into 46, 9 times and leave a remainder of 1. We write 9 on top of the bracket and drop the remainder (1) below the place it belongs.
Step 2) Drop the 5 that is left over in the dividend to form the value 15. 5 goes into 15, 3 times, so we have our final quotient of 93.