Complex Number System Worksheets

The concept of complex numbers was created as a tool to manipulate and understand unique types of equations that contain exponents. These particular equations caused mathematicians a great deal of difficulty because they produce numbers that when squared gave a negative result. Real numbers simply did not apply because negative values do not have a real square root. To tackle this mathematicians created something called an imaginary number which is often signified by the variable i. Imaginary numbers are values that when they are squared produce a negative result. Complex numbers are expressions that contain both real and imaginary numbers. Below you will see a wide offering of lessons and worksheets specific to this topic.

• Adding and Subtracting Complex Numbers - We start out with the easier operations and have some quick successes.
• Calculating Distance in the Complex Plane - The plane makes it very easy to find the value of measures. This is a technique you should use more often. It has many science and technology applications that are used often by engineers.
• Conjugates and Dividing Complex Numbers - This is where it gets a bit more abstract for students. This is a more advanced skill that you will quickly learn to master and use to your advantage.
• Finding the Inverse of a Matrix - We can work with these types of values in a matrix. We show you how to navigate this.
• Graphing Complex Numbers - When you places these values on a graph does it will give you a general idea of how they may physically space out, but not exactly.
• Multiplication of Complex Numbers - This builds off of the addition operation that we have previously visited.
• Polynomial Identities as Complex Numbers - This is a method that can be used to quantify the value of these numbers.
• Rectangular and Polar Forms of Complex Numbers - We move to different forms of these values to help them apply to more disciplines. You will use this in many different physics applications.
• Simplifying Complex Numbers - We look for similarities within the total values. Once we spot it, we reduce those values out of it. This makes it much easier to navigate these values.
• Solving Quadratic Equations - This can take a while to get the hang of. It leads us down the path of understanding these values better. We show you several different ways to manage these problems.
• The Fundamental Theorem of Algebra - A good amount of this is devoted towards the concept of complex zeros.

What are Complex Number Systems?

Complex numbers are one of the building blocks of advanced mathematics and are widely used in algebra. These numbers can be used in solving problems in real life, especially in electromagnetism and electronics.

Complex numbers are made up of two parts: an imaginary number and a real number. We are very familiar with real numbers they can be writing easily on a number line. They come in two forms as rational (can be written as a fraction) and irrational numbers (cannot be written as a fraction). Imaginary numbers are values that when they are squared result in a negative value.

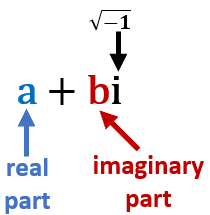
The standard form of a complex number is written as 'a + bi', with 'a' being the real part and 'bi' being the imaginary part. You can see this displayed in the image to right. In these systems either part can be equal to zero. Therefore, any combination of imaginary or real number in this format can be considered as a complex number system. The value doesn't technically signify the intricacy of the system. It means that two types of numbers come together to form a complex.

In this system can consist of any tangible value such as integers, fractions, or countable numbers that can be graphed on the horizontal number line is considered as a real number. Imaginary numbers are more abstract concepts that are employed when the square root of a negative number is needed.

Complex numbers can also be plotted on the two-dimensional plane by plotting an imaginary number on the vertical axis and real numbers on the horizontal axis. the complex number can be denoted by points (a, b). They have many real world applications to model the movement of subatomic particles, modeling the frequency of sounds, and even to understand the relative strength and abilities of electrical circuits.