Multiplying Binomials Worksheets
There are several methods that you can use to multiply binomials, but by far the most valuable method (at the high school level) is the FOIL method. We will therefore focus our effort on centering our lessons around that method. The most important part of this is to make sure that you teach students the language of the FOIL method. What does each letter within the acronym stand for and how does that apply to binomials? It is also very important that students have mastered combining like terms before you start working with this skill. I would recommend a quick review of that skill before you jump in here. It will save both you and students a lot of headaches. This series of lesson and worksheets helps students learn how to find the product of two binomials.
Aligned Standard: HSA.APR.D.7
- Step-by-step Lesson- This lesson examines the basic all-around strategy for developing this.
- Solving Binomial Products Guided Lesson - We throw a bi- to tri- product problem in there too for some review.
- Guided Lesson Explanation - Once you understand how to do the first problem, it just gets easier from there.
- Multiplying Binomials Worksheet 1 - When you push these products together a foil-like method comes out.
- All Multiplication Skills Worksheet 2 - This sheet review the easy and the difficult problems all in one.
- Skill Review Packet - This is a pack of 4 worksheets that span the gamut of what kids really need to know.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
This set follows a stratified pattern of growth of ability on the materials for this section.
- Homework 1 - Find the end product of the two polynomials by multiplying them. This can normally be done in two steps, but a few may be a bit more extended.
- Homework 2 - Multiply the two binomials using proper technique. The first four problems will give you Deja Vu.
- Homework 3 - Another go around with this skill, but we extend the number of terms you have in the expressions.
Practice Worksheets
All the sheets in this series build in skill level and topic knowledge.
- Practice 1 - These might require two or three steps. You will get an idea the minute you start working with them.
- Practice 2 - Remember how to proceed here. Break it apart into several steps and make it work for yourself.
- Practice 3 - The values outside the parentheses is where to start. These can be a bit complicated.
Math Skill Quizzes
These should look pretty familiar to you by now.
- Quiz 1 - Pop these back over time. They will help you learn to break things down.
- Quiz 2 - I wish you could take these over time. Some a pretty simple, other not so much.
- Quiz 3 - Don't let the negative values sour you on these. Just remember a negative times a negative is a positive.
How to Multiply Binomials
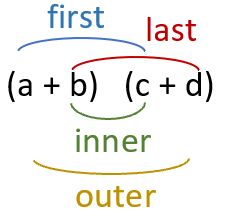
The most common method of multiplying binomials is known as the FOIL method. It is not a necessary method used for multiplication in binomials by following the FOIL order, but using it definitely makes the process easier. The letters in the FOIL method refer to two terms (one of each of the two binomials) which are multiplied together in a certain specified order: First, outer, inner and last. If you following along with the diagram to the right: First (a x c), Outer (a x d), Inner (b x c), and Last (b x d).
For example: (2x + 3) (3x - 1). The following steps will demonstrate how the FOIL method can be used for binomial multiplicand.
1. Multiply the first term of every single binomial. (2x) (3x) = 6x2
2. Now multiply the outer terms (2x) (-1) = -2x.
3. Multiply the inner terms with each other (3) (3x) = 9x
4. Multiply the last terms with each other (3) (-1) = -3
5. List down the results that have been achieved 6x2 - 2x + 9x - 3.
6. Last step includes combining the terms that are similar. Right now, we have the following: 6x2 | -2x | 9x | -3. We can see that -2x and 9x are like terms and can be combined to form 7x. The final value would be: 6x2 + 7x - 3.
When Wil You Use This Skill in Real Life?
Binomials are often used in computer programming scenarios to model the use and execution of commands that the program is to complete. Architects often use the same math to calculate the heights of points in their projects. When economists are trying to determine the trends in the current state of the economy, they will often use binomials to describe events and probability values. During the election in process where often two candidates are seen as the only logical choices, we can use binomial distributions to examine the popularity and potential winner of the race. This math is often used to predict and track the movement of storm systems so that the weathermen can tell you when to wear shorts or bring an umbrella with you to school. As you can see the applications of this type of math is boundless.