Conditional Probability Worksheets
This brings a new range to our understanding of statistics. There will be times where you are evaluating an event that can have the possible outcomes affected by an event that occurred previously. These types of probabilities are referred to as conditional because the outcome of another event (condition) affect the instance that we are trying to determine. The concept may fly over your head, at first, but realize that understanding this can really simplify the calculations that you will need to make in some situations. These worksheets and lessons will help students learn to tackle statistics word problems that include a form of conditional aspect.
Aligned Standard: HSS-CP.A.3
- Economics Class Step-by-step Lesson- See what your chances of taking two classes is.
- Guided Lesson - Do you drink chocolate milk? I do regularly with my grand kids.
- Guided Lesson Explanation - These problems are more common sense with the setup, than you first would think.
- Practice Worksheet - What's the joint probability of playing football and being a girl?
- Matching Worksheet - Eating Chinese food! Who doesn't want some Mo Shu Chicken?
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
You determine and interpret conditional probabilities.
- Homework 1 - The dance teacher teaches two classes of dance (jazz and hip hop). 35% of students attend both dance classes. 40% of students attend just one class of hip hop. What is the prospect that a student that attends the hip-hop class also attends the jazz class?
- Homework 2 - At Xavier's High School, the probability that a student takes Technology and French is 0.082. The odds that a student takes Technology is 0.098. What is the probability that a student takes French given that the student is taking Technology?
- Homework 3 - What is the chance that a randomly selected individual being a girl who drinks coffee regularly?
Practice Worksheets
Yes, I did get a little carried away with my workshops (math, art, science) on this one.
- Practice 1 - Two math workshops were organized by the Math club. The first workshop was attended by 20% of the High School students. Both the workshops were attended by 45% of the High School students. What percent of those who attended the first workshop also took part in the second?
- Practice 2 - A photography competition was organized by the middle school. The competition was organized in two parts. The first part, drawing, was attended by 15% of school students. Both the workshops were attended by 66% of the Middle School students. What percent of those who attended the first workshop also took part in the second?
- Practice 3 - What is the plausibility of randomly selecting a child that plays tennis?
Math Skill Quizzes
These sheets ask you to determine the probabilities of everything here.
- Quiz 1 - On a shelf there are novels and spiritual book. Two books are chosen at random without replacement. The possibility of selecting a spiritual book and then a novel is 0.83. The prospect of selecting a spiritual book on the first draw is 0.97. What is probability of selecting a novel on the second draw?
- Quiz 2 - What is the expectation of randomly selecting an individual that is a boy?
- Quiz 3 - What is the probability of a randomly selecting a girl?
What Is Conditional Probability?
Conditional probability is defined as the possibility for the likelihood of occurrence of an event based on the occurrence of the previous outcome. There is a set condition that this probability value hinges upon. This allows us to evaluate how our previous experiences can and will affect our future experiences.
To calculate conditional probability, we multiply the probability of the previous event by the probability of the next event. For example: Event A represents that it is raining with 0.2(20%) chance of raining today. Event B is that you be required to go outside with a probability of 0.6(60%). A conditional probability will see into these two events with a relationship to one another. That is the probability that represents both, you need to go outside, and it is raining.
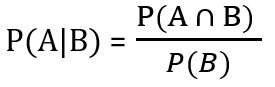
The conditional probability formula helps us determine this measure. The numerator of the formula is the cumulative probability that event A and B happen together. The denominator is just the probability of event B occurring. This provides us with a context of how many total samples spaces there are, this accounts for the total number of occurrences.
Remember as we have discussed previously that you must first diagnose the nature of the relationship between these events that we are evaluating the probability. How we calculate their values will depend on this.
Independent Event - Independent events are events that are not affected by one another. For example, tossing a coin. In a coin toss, each toss is an independent event and an isolated outcome.
Dependent Event - Events can also be dependent. That is, both the events are affected by each other. The next event is affected by the probability of the previous event. For example, 2 blue and 3 red balls are in the bag. The probability of getting a blue ball is 2 in 5. But if we got a red ball before, then the probability of getting a blue is 2 in 4.