Volume of Cones and Spheres Worksheets
Volume is how much space something occupies. These two three-dimensional geometric shapes have a very unique relationship when it comes to volume. A cone has a flat circular base that joins together into narrow point at the other end. Cones have two faces and one edge. A sphere is rounded three-dimensional shape that does not have any vertices or edges. Spheres have a single continuous face. The volume of a cone occupies one-third the volume of a cylinder. The volume of a sphere occupies two-thirds the volume of a cylinder. When you combine (add) their volumes it is equal to the volume of a cylinder. These worksheets and lessons will show you how to calculate these measures and help you make sense of it all.
Aligned Standard: High School Geometry - HSG-GMD.A.3
- Cone Volume Step-by-step Lesson - Figure out the volume of an old fashion ice cream cone.
- Guided Lesson - Cones and spheres all around. What's their volume?
- Guided Lesson Explanation - These problems and the unit, for that matter, are mostly plug into the equation and go.
- Practice Worksheet - Work yourself into surface area.
- Matching Worksheet - I left the units off because it just won't fit without looking chaotic.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
A page donated to each skill and then a cumulative page for you.
- Homework 1 - The formula of volume of cone = 1/3 Π r2h. You will get practice solve a bunch of problems along the way.
- Homework 2 - The formula of surface area = 4 Π r2. We calculate these measures on the surface of a sphere.
- Homework 3 - Put this together to find the radius in each case. We apply this to both geometric shapes and learn all their measures.
Practice Worksheets
Cones, cones, and more cones!
- Practice 1 - What is the volume of this cone? Use the techniques that we have discussed here.
- Practice 2 - What is the surface area of this sphere? Make sure that you round your answer to the nearest hundredth.
- Practice 3 - More problems that will challenge you. This provides you with more practice.
Math Skill Quizzes
The difficult is somewhat even across all of these.
- Quiz 1 - Pay attention to the height value. This quiz covers all the skills we are working on.
- Quiz 2 - The radius and height of the cones are provided. Work off of them to fins the measures we are looking for.
- Quiz 3 - You will be asked to round your answer to the nearest hundredth. Remember that this is two places to the right of the decimal.
How to find the Volume of Cones and Spheres
We all have enjoyed ice cream cones and kicking the ball around in the park. But do you know we have a different name for the geometric shape for your favorite ice cream cone and basketball? The geometric shape of your favorite ice cream cone is termed a cone, which makes sense. The geometric name for a basketball shape is known as a sphere.
Cone Shapes - A cone is a 3D shape that has one edge and two faces. Generally speaking, they have a point at one end and a circle at the other end. Unlike most shapes, they are not a polyhedron, which means that it doesn't have flat faces. Its circular and pointy ends are completed with a curved surface. The flat part is known as the base, and the pointy end is termed as the apex.
Volume of a Cone - There are many times that manufactures of cones need to know how much space the cones occupy, especially when packaging ice cream cones to send to your home. This measure is known as volume.
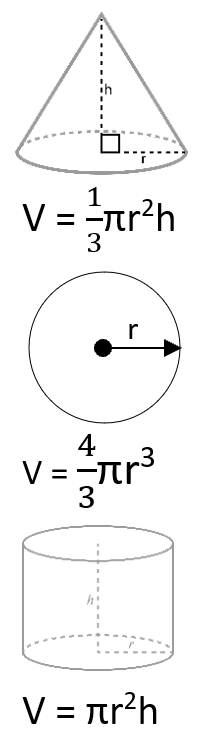
To find the volume of a cone, we use the formula: V = 1/3 x Π x r2 x h
Where 'r' is the radius of the circle at the wide end and 'h' is the height.
Spheres - A perfectly symmetrical 3D shape with one continuous surface and zero edges or vertices. Spheres, unlike cones, are not a polyhedron. Every point on the sphere's surface is equidistant from its center. Like a 3D circle.
We calculate the volume of the sphere by using the formula: V = 4/3 x Π x r3. Where 'r' is the radius of the sphere.
Relating Cylinders - The formula for the volume of a cone and a sphere are related to the volume of cylinder. In fact, when you combine (add) the volume of a cone and sphere they equal the volume of a cylinder.
Volume of a cylinder is: V = Π x r2 x h
Let's Take a Look at These Geometric Shapes
An ice cream cone basically sums up these two geometric shapes in one. Take a look at the image below to see what we are saying.
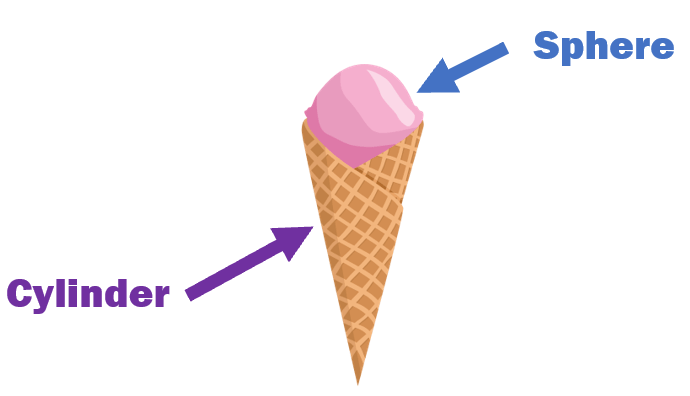
If you think about it where else do you see these shapes, how many can you name? Here are ten common examples of cones that you will come across in your daily routine: party hats, street cones, volcanoes, most trees, a megaphone, teepees, Bugels snacks, most costume noses, a tip of a pencil, dog head cones to protect them from licking themselves. How about spheres, that is a little easier. Here you go: an orange, a class globe, the sun, lollipops, basketballs, baseballs, bowling balls, planets, moons, marbles, and an eye ball.