Corresponding Angles and Sides Worksheets
Triangles are super cool and really helpful in the everyday world. When just about anything is being constructed one of the critical phases, very early on, is called surveying. A surveyor constructs a basic blueprint of the entire construction area that is being worked on, not just where the project is being erected. This tells the general contractor the features of the environment and what they must contend with in order to build the structure blueprints and actually begin building it. In order to prepare these maps, if you will, surveyors use a method called triangulation that measures the angles in a triangle around three survey points on the job site. They then need to measure just one side of the triangle to determine the length of the other two sides. These worksheets show students how to locate and use corresponding angles to your advantage when you have two similar triangles.
Aligned Standard: High School Geometry - HSG-SRT.A.3
- Similar Triangles Step-by-step Lesson - See if this one makes sense to you. It works pretty well in practice.
- Guided Lesson - A blender like set of problems for you to work on.
- Guided Lesson Explanation - All the answers are some what related to same primal concept.
- Practice Worksheet - I blew up all the shapes to make them readable and easier to work with.
- Matching Worksheet - You could get away with only doing two, but that would be no fun.
- Finding Sides of Similar Triangles 5 Pack - Given similar triangles, what can you find value in?
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Find all the missing sides and angles that we see in the similar triangles.
- Homework 1 - We need to find the missing length.
- Homework 2 - You should remember that the sides of similar triangles are proportional.
- Homework 3 - Start by stating what you are looking for.
Practice Worksheets
These problems have some really significant real world value.
- Practice 1 - In the diagram below, ΔIJK ≈ ΔLMN. Find c.
- Practice 2 - The original diagram included a smaller triangle inside a larger triangle.
- Practice 3 - When two triangles are similar, we can find many different matching parts.
Math Skill Quizzes
Even though the quizzes are only 4 questions long, they can take a good bit of time to do.
- Quiz 1 - If BC=6, PQ=7, AB=10 and PR=8, find the value of QR.
- Quiz 2 - In the figure given, ΔMNO is similar to ΔHJI . If MN=16, HI=27, ON=22 and IJ=18, find the value of MO.
- Quiz 3 - Find all the missing sides by using the information that are given to work with.
What are Corresponding Sides and Angles of Triangles?
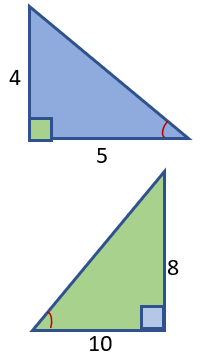
We know what similar figures are now, don't we? If you don't remember, we'll take a quick review. When two figures are exactly the same, with similar measurements and equal angles and their sides are proportional to one another they are known as similar figures. Take a look at an example. Please note that to save space, these are not drawn to scale. When you draw two triangles with the same exact angular measurements this indicates that all the angles are corresponding. In this case we can see that both triangles are right triangles and have a corresponding angle, this means that the third angle must be congruent as well. The length of sides does not need to the same, but they must be proportional to one another to be consider corresponding sides. In this case the sides lengths are in a 4:8 (opposite side) and 5:10 (adjacent side) consistent proportion. With these two facts in hand, we can confidently say that these triangles have both corresponding sides and angles.
Now, look at the corresponding sides of the triangle. The angles that they form are perfectly similar, and this set of angles is known as "The corresponding angle." Regardless of how rotated the triangles are, whenever their sides match, their matching corners will form angles, and they are known as corresponding angles. Corresponding angles are also formed in the matching corners of other different shapes. Squares, rectangles, and more, corresponding angles are formed in every shape! This also means that when we have triangles that meet both of these parameters, we can classify them as being similar. When we are able to determine this to be true, we can use that fact to better understand all geometric figures that reside in the same vicinity. This means if you know the dimensions of figure like this in the real world you can use that information to infer the height of a surrounding tree, building, radio tower anything that is difficult to measure by hand. Just think of the time you will save carrying a ladder that is that size. Ladders made for that purpose take a day for a crew to just setup.