Dilation of a Line Segment Worksheets
You may have had a physician shine a light into your eyes and wonder what the purpose of that was. The doctor is trying to dilate your pupils so that they could examine they could evaluate the full eye. When your pupils are dilated, they become larger, as a result, more light is allowed in which allows the doctor to see what is inside. In geometry dilation is when something either becomes larger or smaller. The important part to note here is that when dilation occurs the proportions remain the same, just the entity is changed by a scale factor. In this section of worksheets and lessons we will focus on how this can be applied and understood in regard to lines and line segments. These worksheets and lessons help students learn how to go about dilating a line in several situations.
Aligned Standard: High School Geometry - HSG-SRT.A.1a
- Write the Equation Step-by-step Lesson - We pack you in here to rewrite an equation of the line after a dilation.
- Guided Lesson - This lesson can take some kids half an hour to manage properly.
- Guided Lesson Explanation - These problems took me about 2 hours to explain properly, see if it worked out.
- Practice Worksheet - Scale factors come into play here to work the line.
- Matching Worksheet - This could take an hour or so to complete.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
It is all about writing the equation for the lines and making adjustments.
- Homework 1 - In most circumstances it is best to start with the y-intercept.
- Homework 2 - Write your answer in slope-intercept form.
- Homework 3 - Where is the origin in reference to the line?
Practice Worksheets
Scale factors tend to throw kids for a loop. Help center them on the concept.
- Practice 1 - Write the equation of the image of l after dilation with a scale factor of 4, centered at the origin.
- Practice 2 - Use the graph to get a visual understanding of the system for yourself.
- Practice 3 - This line strikes the origin.
Math Skill Quizzes
The quizzes build in a progression. They are much easier to work on in order.
- Quiz 1 - Make fully sure you understand the parts of the linear equation.
- Quiz 2 - These can be pretty easy to navigate if you break them down.
- Quiz 3 - The strike through the origin gives you a grounded model to work with here.
What are Geometric Dilations?
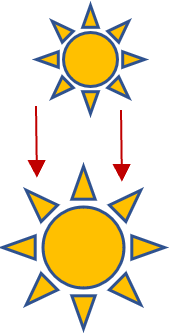
A transformation that can change the length of all line segments by the same proportion is known as dilation. Dilations do not change figures; they change the size. They adjust it by a scale factor that either scales it up or down based on the value of the factor. They are commonly written in a decimal such as 1.5. This value indicates that the figure would increase by 50%. It can also be written as a standard proportion. For example, a scale factor of 1.5 could also be written as 2:3.
In very simple words, when talking geometrically, dilations refer to making something change its sizes. The shape of the figure is not altered, only the sizes are changed i-e: the images can become either bigger or smaller. For completing a dilation, two things are needed. A fixed point or center point and scale factor or ratio. If the absolute value of the scale factor is less than 1, then the image is small and if the value is greater than 1, then the image will be large.