Graphing Square and Cube Root Functions Worksheets
When we graph these types of functions, they give off a characteristic pattern and shape. As you become more proficient with this skill you will be able to match the graph to equations just by how it spreads out when drawn. In this section we will explore how to determine the equation of square and cubed functions from their graph. You will also learn how to solve linear equations that can be formed from evaluating these types of functions. A selection of worksheets and lesson that shows students how to create and read a graph of a square or cube root.
Aligned Standard: HSF-IF.C.7b
- A Graphed Square Root Step-by-step Lesson- What is the equation for the graph?
- Guided Lesson - This includes graphing, equation solving, and graph interpretations.
- Guided Lesson Explanation - One and three are really long problems. Number two is only a line or two.
- Practice Worksheet - Students have the most difficulty with the equation deciphering.
- Matching Worksheet - I tried to write a nice review problem for students here.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Cubes are a bit uncommon in the real world. You will see many more use of the squares.
- Homework 1 - Solve the given linear functions f(x) = √x2 + 5 and the draw graph for the given function.
- Homework 2 - We find the plotting points of the given inequality equation.
- Homework 3 - We are going to find out the plotting points for given equation. In the first step, we are going to change equation in the form of y = mx + c.
Practice Worksheets
These questions build as you continue through them.
- Practice 1 - Solve the given linear functions f(x) = x + 5 + 3 and the draw graph for the given function.
- Practice 2 - What is the equation of the square root function in the graph below?
- Practice 3 - Not simple, but it can be done.
Math Skill Quizzes
We ask you to draw functions and then interpret them.
- Quiz 1 - Solve the linear functions f(x) = x + 8 - 9 and the draw graph for the given function.
- Quiz 2 - You might be able to just eyeball this one.
- Quiz 3 - What are you thinking with this quiz?
How to Graph Squares and Cube Root Functions
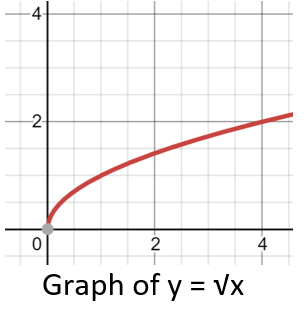
When we are preparing to create a graph for any linear equation, we follow the same process. We place arbitrary values for x into the equation and determine our y values to generate a set of order pairs that fall on the line of the graph of the equation. We then plot those order pairs and connect them to form the line of our graph. We follow this same technique when we are graphing functions.
A basic square root function has a variable under the square root symbol somewhere within it. Similarly, a cube root function has a cubed root located within it. The basic functions of these roots are denoted by √ (x) and 3√ (x). These functions can be graphed by finding certain points that can satisfy every single point, thereby generating ordered pairs, plotting and connecting the dots. It all starts by identifying the algebraic operations in terms of their corresponding transformations. Now you take the graph of the basic function and based on their relative transformations in order horizontal, reflections, shrinking/stretching, vertical.
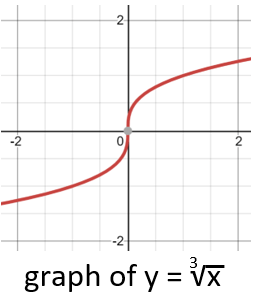
There are some characteristic shapes of graphs of certain functions. A square root function has several unique characteristics. Unless the domain is altered, square root function will have an x and y-intercept of 0. Meaning that it will always have a point at the origin (0,0). Square root functions such as the graph of y = √x (to the right) begin at the origin (0,0) and consistently rise across quadrant I of the graph. Graphs of cubed functions also have the same pattern, but in both directions. The same shape as a square appears in quadrant I and a mirrored image of it appears in quadrant III as you can see on the graph. The third quadrant appears in the fashion because unlike the square function, cubed functions can process negative values.