Using the Quadratic Formula Worksheets
The quadratic formula gives us a quick and easy way to find the roots of a second order polynomial. They help us solve those values when the quadratic equation follows the form of ax2 + bx + c = 0. We can often rearrange equations to fit this form, so this can be a very helpful formula. The roots that you end up determine tell you where the graph of this equation crosses the x-axis. In this section of our website, we will present you with a number of problems that will help you practice this skill.
Aligned Standard: HSA-REI.B.4b
- Solve for y Step-by-step Lesson- See the quadratic formula in action here.
- Guided Lesson - Find the value of the variables using the quad. formula.
- Guided Lesson Explanation - Once students get the hang of using the formula, it becomes second nature.
- Practice Worksheet - Yes, there is a similar theme among these problems. I find this theme helps them grasp the technique much faster.
- Matching Worksheet - Match the variable's value to the quadratics.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
This is an important section for students. They can use all the practice that they can get.
- Homework 1 - Where a ≠ 0. We can use it to solve a quadratic equation (ax2 + bx + c = 0).
- Homework 2 - Now we will use the quadratic formula to solve 5y2 + 5y – 5 = 0.
- Homework 3 - In this case a = 1 b = -4 c = 2. We plug those values in the formula we have been using.
Practice Worksheets
This skill is found in so many different forms of science that it is key to motion in many respects.
- Practice 1 - Solve the equations using the quadratic formula.
- Practice 2 - Just plug and chug away at this formula.
- Practice 3 - Solve for each variable using the quadratic formula.
Math Skill Quizzes
My husband was a salesman for years and always used the quadratic formula to forecast sales.
- Quiz 1 - This technique is used often to gauge the speed of UFOs.
- Quiz 2 - Most economists used this formula to predict profits.
- Quiz 3 - When the equipment is down in a submarine, the quadratic formula is used to determine the impacts of torpedoes.
How to Use the Quadratic Formula
The easiest way to solve the quadratic equation is to factor the quadratic for the value of 'x.' We equate each factor equal to zero and then find the solution for each factor. Where factoring seems challenging, the quadratic formula makes it easier to find the solutions. If you use the general quadratic equation, ax2+ bx + c = 0. Then you will be able to find the roots of the quadratic equation i.e., values of 'x' for which the equation is being solved. The Quadratic Formula also uses 'a', 'b', and 'c' to represent the numerical coefficients. They are known values. It should also be noted that a cannot be equal to 0. The Quadratic Formula can be written as:
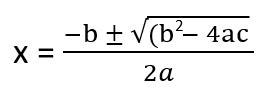
One of the best ways to better understand how we can use this formula to solve quadratic equations is just to put it to work for itself. What if you were asked to solve the quadratic listed below?
x2 + 4x - 5 = 0
Identify Values of Coefficients - First, identify the values for a, b, and c. Make sure you write you work off of you equation in the format of quadratic equation, i.e., ax2 + bx + c = 0. It is already in that format for us. a is the coefficient that is located with x2. There is no value located there which means that is equal to 1. So, a = 1. b is the coefficient found in from of the x, in this case b = 4. c is the constant that is found on the backend when they are written in standard form, in this case c = -5.
Plug a, b, and c Into Quadratic Formula - We just take those values that we have determined and place them into formula: a = 1, b = 4, and c = -5:
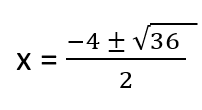
Based on this x would either equal 1 or -5. These solutions indicate the x-intercepts of the equation. That means that when we graph this equation we will know where it crosses the x-axis. Remember that because of the plus/minus sign you will always have two solutions to be worried about.