Interpreting Slope and Intercept Worksheets
The linear form of equations involves two commonly held variables (m and b) and they produce a straight line when plotted on a graph. Those two variables indicate significant features about that line. Linear equations are often written in slope-intercept form in the general form of: y = mx + b. The variable (m) indicates the slope which indicates the steepness or pitch of line. The more positive the value of the slope, the steeper upward the line is. The more negative the slope value, the steeper downward the tilt of the line will be. The variable (b) indicates where that line will cross the y-axis or where the position of the x variable is equal to zero. Students quickly learn with these worksheets and lessons on how to use slope and y-intercept data to better understand data sets and linear equations.
Aligned Standard: Grade 8 Statistics & Probability - 8.SP.A.3
- Make a Scatter Gram Step-by-Step Lesson- This is a very basic one just to get the ground work started for kids.
- Guided Lesson - Graph a function, calculate slope, and make another scatter gram while you're at it!
- Guided Lesson Explanation - I find this skill to just be a culmination of skills that kids have learned earlier in the Core.
- Independent Practice - Three pages of sheer practice. After finishing this your students should have a good handle on the concept.
- Slope of a Line Five Pack - We give you two points that are on a line; tell us the slope of that line.
- Find the Intercepts Five Pack - Find the x and y intercept of these lines.
- Matching Worksheet - Find the slope of the graphs.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Making scatter grams, graphing functions, and calculating slope.
- Homework 1 - The table below displays the data of apples eaten by Travis in a week. Make a scatter gram of this data.
- Homework 2 - We make up values for x and in the process we calculate the value of y.
- Homework 3 - We find that two points on the line are (4,6) and (2, 2). Now we will put the points in slope formula.
Practice Worksheets
Time to create your own data charts from collected data.
- Practice 1 - The table below displays the upcoming results of class 8th. It displays the number of students in each group.
- Practice 2 - Make graph using this function: y = x + 8
- Practice 3 - Calculate the slope of the graph.
Math Skill Quizzes
A similar set of skills is tested here. The scatter grams are fun and helpful.
- Quiz 1 - We are given the inventory data of a cell phone shop. You have to make a scatter plot according to the data of the cell phones and cell phone boxes.
- Quiz 2 - Determine the slope of the line that passes through the points - (-11,6), (5,-5)
- Quiz 3 - Find the slope of any graph on this section.
How to Find the Slope and Intercept of a Line
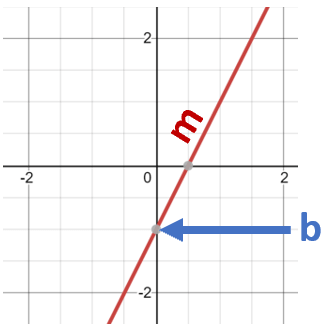
When we are learning concepts in coordinate geometry, the slope and y-intercept are the first ones that we come across. These are two of the most critical elements of understanding the significance of equations of lines.
Slope - The slope is a measure of the steepness of a line. It is the ratio that is determined as rise over run. This measure gives you an understanding of tilt of the line. Two parallel lines have the same slope, and the slope of two perpendicular lines are negative reciprocals of each other.
Y-intercept - The y-intercept is the point at which the line cuts the vertical or y-axis. An equation of a straight line is found in the form of: y = mx + b. This form of an equation is called the slope-intercept form because both of those measures are expressed directly in the equation itself. In this form the coordinates are dictated by the x and y positions. The variable "m" is used to indicate the slope, and the variable "b" is the y-intercept.
Take a look at the plotting of the line y = 2x – 1. We can see that the line crosses the y-axis at -1 which indicates the intercept (b). The lines steepness (slope or m) is listed as 2 and can be found in that ratio and can be checked by taking two point on that line.
There are two primary methods for determine the slope of a line and determining the position of the intercept:
Method 1: Using the Graph - You can use the graph to calculate the slope and y-intercept. Take two pairs of co-ordinates to calculate the slope. The formula to calculate slope is: m = (y2 - y1)/(x2 - x1). Simply substituting the coordinates in the formula will help you calculate the slope of the line. For the y-intercept, you can analyze the graph and see where the graph cuts the y-axis.
Method 2: Using the Equation - When you use the formula to calculate the slope, you can then use the equation of the straight line to calculate the y-intercept. You substitute the value of m by the slope you calculate, choose a pair of coordinates on the line and substitute the variables x and y with the coordinates. It will help you calculate the y-intercept.