Similar Figure Worksheets
In geometry we are constantly attempting to understand unknown or missing measures. It can be an angle, side of a shape, or even a length of a line. There are many different ways we can go about determining those measures, but we can often use other shapes that are floating around in a similar system to help us determine these measures. The relationship between two geometric figures that have the same shape is referred to as similar. They can be a different size, but they do share the same shape. There are two fundamental things that we know about similar shapes: their corresponding sides and angles are also equal. Corresponding means that the side or angle is found in relatively the same location in a two-dimensional space. When we can identify the existence of this, we instantly can find the measure of missing sides or angles. These worksheets and lessons will help you learn to identify similarity between various geometric figures and learn to use that within the scope of geometry.
Aligned Standard: Grade 8 Geometry - 8.G.A.4
- Explain Congruence Step-by-Step Lesson- We go over all the things you need to know about congruent and similar figures.
- Guided Lesson - This somewhat mimics the previous standard in a lot of ways (G.3).
- Guided Lesson Explanation - A very basic explanation will do it for this one. It should be easy to follow.
- Independent Practice - How did one shape become another? Untwist the plot of these shapes on the grids.
- Matching Worksheet - I know it would have helped if I used the same shape over and over, but this gives students some confidence.
- Exploring Similar Figures Five Pack - It is amazing what you can get out of two similar figures.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Each sheet builds upon the last sheet.
- Homework 1 - The figures have been dilated with a scale factor of ½ then reflected across the x-axis, making Figures B and B' similar, but not congruent.
- Homework 2 - In this case, the scale factor of the dilation can be found by using the horizontal distances on the triangle. 90° clockwise rotation, translate 2 right and 4 up, dilation of 1/2.
- Homework 3 - Dilated with a scale factor of 4/2 then translate 3 right and 3 down, making Figures X and X' similar. Since the shapes are not the same size, they are not congruent.
Practice Worksheets
Most students claim that these get progressively easier.
- Practice 1 - Describe the sequence of transformations that results in the transformation of Figure A to Figure B.
- Practice 2 - Figures are congruent if they are the same exact shape and size. Figures can be similar if they are the same shape, but different sizes.
- Practice 3 - Is Figure Z congruent to Figure Z'? How do you know? Explain.
Math Skill Quizzes
These are all about identifying corresponding angles.
- Quiz 1 - Which angle corresponds to
- Quiz 2 - What is the ratio of side AB length to the length of its corresponding side?
- Quiz 3 - Which angle corresponds to
What are Similar Figures?
There are all types of different geometric shapes that you will come across in your everyday life. You will see different shapes such as rectangle, squares, triangle, pentagon, and hexagons. When we see two shapes that share the same form, but not necessarily size we refer to these two shapes as being similar. In more depth, two figures are similar if their angles and the ratios of the length of their corresponding sides are equal too. This means that they are at an equal scale or ratio to one another. This means that sides will be in a fixed proportion to one another.
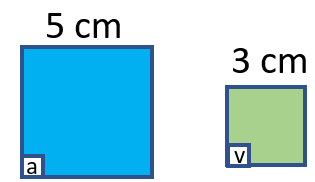
As a result of this similar figures share corresponding sides that are equal in ratio to one another. The corresponding angles of these shapes are also equal. If you take a look at the squares below, you can note that are similar in a scale factor of 5:3. This means that angle b and v are equal because they are corresponding (in position).
Have you ever seen an architectural model of a building? In most cases those models are created in an exact scale to the actual buildings themselves. This way you can mathematically see how this structure will fully appear after being constructed. This is the concept of scale. The model is a similar figure to the final building.
The symbol we use in geometry for denoting similarity between figures is "∽". You will see this symbol used all the time within geometric proofs. We use geometric proofs to prove concepts in math and one of the fundamental properties we often use to relate two figures is similarity. If this property does exist between 2 geometric shapes, we can easily determine the length of a side or the measure of a missing angle.
To understand better, look up identical twins! They are the perfect example of what similar figures are, but in the human sense.