Dilations, Translations, Rotations, and Reflections Worksheets
When we are describing a geometric shape, we will often need to describe the movement of that shape in a clear and concise manner with one another. These movements of geometric figures are called transformation. There are four very commonly types of transformations. When only the position of shapes has changed and it acts as if it were slid across the floor, we call this translation. If the figure was turned around the center of itself, like a wheel on a car, we call this a rotation. If a figure is moved in such as way that it looks like a mirror image or a flip across a line, we call this a reflection. In all the instances that we have described such far the shapes remained the same size. If the shape increases or decreases in size without the shape changing, as if it were inflated or deflated, we call this change a dilation. On this page you will find a ton of worksheets and lessons to help you learn how to describe the movement of geometric shapes properly.
Aligned Standard: Grade 8 Geometry - 8.G.A.3
- Translating Points Step-by-Step Lesson- Take a point. Move it around a grid system based on directions.
- Guided Lesson - This one really measures if you are paying attention to what you read. I would advise you to read each question twice.
- Guided Lesson Explanation -We work with flips and all kinds of other moves across the board here.
- Independent Practice - This one reminds me of the game battleship!
- Matching Worksheet - Some students find this a bit complicated. It does mirror question types that I have seen before on this skill.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Each sheet is focused on a specific type of transformation and offers you two visual problems.
- Homework 1 - What will be the coordinate if the point R (2,-2) is translated 3 units left?
- Homework 2 - If the point R (4, 3) is reflected over the y axis, what will be the coordinates of the resulting point, R’?
- Homework 3 - A reflection is also called a flip. It is to flip over the y-axis. The point is currently 4 unit away y-axis origin.
Practice Worksheets
We work with scale factors and point movements.
- Practice 1 - Graph the image of triangle ABC after dilation with the scale factor of 3, centered at the origin.
- Practice 2 - What will be the coordinates of the point Q' if the point Q(1, -3) is rotated 270˚ counterclockwise around the origin?
- Practice 3 - What will be the coordinate if the point H(-2, 2) is translated 5 units right?
Math Skill Quizzes
Time to play "What are the coordinates when point x is ..."
- Quiz 1 - What will be the coordinate if the point A (-1, 4) is translated 2 units left?
- Quiz 2 - If the point D(4, 4) is reflected over the y axis, what will be the coordinates of the resulting point,D'?
- Quiz 3 - Graph the image of parallelogram ABC after dilation with the scale factor of 2, centered at the origin.
What are Dilations, Translations, Rotations, and Reflections?
In geometry, changing the position of a geometric shape is referred to as transformation. Transformations are broadly broken into four types: dilation, translation, rotation, and reflections. In some transformations, the position is changed but the size is maintained. Examples of this type of transformation are: translation, reflections, and rotations. Dilations are transformations that alter both their position and size.
Translation - This type of transformation slides the figure through space or across a plane. All points that compose the figure move simultaneously to the same distance and travel in the same direction. This is as if it was slid across a patch of ice. To simplify it for you, translation is the change in location, which is specified by a distance and a direction. As we can see with the example of the triangle below, every point in the shape was moved in a Northeast direction at the same distance.
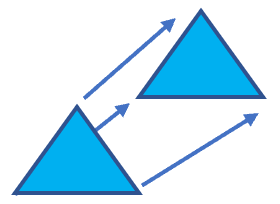
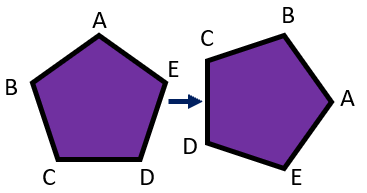
Rotation - Rotation, as the name implies, turns the figure around/about a line or point. It essentially spins the shape around. The point at which the figure is turned is known as the center of rotation. The center of rotation can be located inside or outside the shape. Remember that rotation means to turn a figure about / around the center of it. We see this movement all time in our typical day such as in the movement of a bicycle or car tire, in a pinwheel, or even a Ferris Wheel. As a result of turning on this center, every point within the shape stays the same. If we look at the purple pentagon below you, we see a 90-degree rotation.
Reflection - We have all studied reflection in science. Let's get familiar with its mathematical aspect. In geometry, reflection means to transform a figure in a way that it is flipped across a line. You might have noticed some figure that remains the same even if they are flipped over a line. This means that such figure can be folded along a line and have exactly same halves. Such shapes exhibit reflectional symmetry, and the line folding the paper is termed as a line of reflection. If you take a look at the image of a calculator on the right (below), you will see a reflection positioned to the left of it.

Dilation - Dilation retains the shape of the shape while altering the size of the shape. Dilation of a figure can be of two types; reduction and enlargement. Enlargement means to increase the shape of the figure. If we think of a shape that is an inflatable balloon this is when we add air to it. While reduction means to decrease the size of the figure. In the case of the same balloon, this is letting air out of the balloon. The scale factor determines how much the size is reduced or enlarged. If we take a look at the smiley face below, we can see dilation and the arrows indicate reduction and enlargement.
