• Decimal-Fraction Step-by-Step Lesson- Convert a decimal to a fraction and then bring a decimal to life.
• Guided Lesson - More decimal / fraction conversions and we have you label numbers as rational and irrational.
• Guided Lesson Explanation - I spent a good amount of time on the concept of rational numbers. Hopefully you find it helpful.
• Practice Worksheet - A real obstacle course of problems for you. I find these types of problems to be very paper dependent, meaning you should have some scrap handy.
• Matching Worksheet - A great refresher or warm-up for students that have mastered this skill.

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

The lesson focuses on decimal fraction conversions and we work into irrational numbers later.

• Homework 1 - Every place to the left and right of the decimal point has a name.
• Homework 2 - Do the actual math and divide as the problem states: 19/100 (2 zeroes = move the decimal to the left twice).
• Homework 3 - Every place value name dictates the fraction.

Practice Worksheets

These sheets are very mixed with different types of problems. I thought it was time.

• Practice 1 - Write 0.11 as a fraction.
• Practice 2 - Label the number rational or irrational: 481216.
• Practice 3 - Write the fraction 52 / 100 in decimal form.

Math Skill Quizzes

These are a bit decimal-fraction centered. The last quiz has irrational numbers.

• Quiz 1 - Change 0.15 to a fraction.
• Quiz 2 - If you were to name this number it would be nine-tenths.
• Quiz 3 - We add the concept of radicals to the fore front.

Methods to Express a Repeating Decimal Value

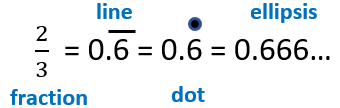
There are three widely accepted methods you can use to express a value that ends in a repeated value. You can see all three displayed to the right. a) Horizontal Line - Probably the most commonly used symbol is the horizontal line over placed over the integer that repeats. b) The Single Dot – This is similar to the line being over the repeating digit, but instead of a line you have a thick dot. C) Ellipsis – An ellipsis (…) is punctuation mark that is often used in literature to create to create somewhat of a pause or fade out effect. You will find those three trailing dots used often to indicate recurring decimals in values that are found in literary works.

What are Irrational Numbers and Decimal Expansion?

Irrational Numbers - Irrational numbers are real numbers that you cannot express as a ratio of two integers. One of the perfect examples of an irrational number is Pi (3.14159...). It is a common example given for an irrational number. The reason behind this is that it doesn't have a finite number of digits after the decimal.

Many square roots are irrational, as they cannot be further reduced to fractions. For example, √2 is close to 1.4.14, but there is no proper or predetermined value for it as there is an infinite number of digits after the decimal point. This value cannot be expressed as a fraction because its square root is irrational.

If a number can be expressed as the ratio between two integers, it is called a rational number. Some of the examples of an irrational number are √2, 3.14, √3, and ℼ.

Decimal Expansion - Decimal expansion of a number is its representation in base of 10 (i.e. decimal system). This may seem complicated, but you are just taking a whole number or fraction and presenting it in decimal form. In the decimal system, every decimal place consists of digits that range somewhere between 0-9 arranged in such a way that every digit is multiplied by the power of 10, decreasing from left to right. For example, the decimal expansion for 1234.56 will be defined as:

1234.56 = 1 x 10³ + 2 x 10² + 3 x 10¹+ 4 x 10⁰ + 5 x 10^-1 + 6 x 10^-2 = 1 x 1000 + 2 x 100 + 3 x 10 + 4 + 5 x 1/10 + 6 x 1/100

You will find this a very helpful form of notation as you advance further will science class. When you need to express very large or very small values, this makes it easier to track for certain.