Comparing Properties of Two Functions Worksheets
In math we use functions to model situations or phenomena that is consistent. While there may be some limits to the level of accuracy that be exhibited, they are very help for understanding a scenario and predicting changes that can be made to improve an outcome. There will be times when you have multiple options of how you can use a function and analyzing and comparing those possible uses of functions can indicate which would be best for our situation. We lean heavily on the use of graphs to understand the nature of functions, but they are not always practical solutions. In this section we will focus on analyzing function tables and algebraic comparisons. These worksheets and lessons teach students how to compare the various properties of functions.
Aligned Standard: Grade 8 Functions - 8.F.A.2
- Compare the Functions Step-by-Step Lesson- You are provided two functions in equation and table form. Compare them as best you can.
- Guided Lesson - We look at positive and negative slope and what it means about the relationship between the two functions.
- Guided Lesson Explanation - These problems involve a great deal of slope calculations. Make sure your students have that skill down pat before moving on to this skill.
- Independent Practice -Not only are the problems themselves lengthy, the answers take up a great deal of paper to solve.
- Matching Worksheet - Solve all the word problems to find their match. This one only has 4 problems because of the sheer volume the problems take up.
- Co Functions Worksheet Five Pack - This pack and the next is here to show you the next level of material that is coming up for this topic.
- Composition of Functions Worksheet Five Pack - This really boils down to the old plug the numbers in and solve type of problem.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Compare the functions and the input/output charts for slope.
- Homework 1 - The equation of straight line is y = mx +b Slope is the rate of change. The coefficient of x is the slope of the line.
- Homework 2 - Compare the two linear functions listed below and determine which has a negative slope.
- Homework 3 - Will is a shop keeper. He has 25 toys at the start of the day. He sold 5 toys per day. Write the rule for the total number of sold toys as a function of the number of days (d). c = 25 - 5d
Practice Worksheets
This is a skill that covers a lot of ground and can be interpreted many different ways.
- Practice 1 - Roy starts with $100. He spends $10 per week. Let y be the amount remaining as a function of the number of weeks, x.
- Practice 2 - Determine which has the greater rate of change.
- Practice 3 - Compare the following functions to determine which has the greater rate of change.
Math Skill Quizzes
The variable g(x) is introduced and sometimes it will make the kids' heads' spin
- Quiz 1 - Compare the following functions to determine which has the greater rate of change.
- Quiz 2 - Using f(x) = 5x + 5 and g(x) = x + 2, find: f[f(3)]
- Quiz 3 - Simplify Cot (90-x) tan x
How to Compare the Properties of Two Functions
A function is a mathematical relationship that takes in an input and based on the rule that is assigned will produce an output. They are a concept which needs to be adequately understood so that it doesn't create problems in the future. Most students might not know that this concept will get more difficult as you move to higher classes. Functions can be represented in many different ways. The most common ways to illustrate them is through the use of an input-output table, equation, or graph. There are three ways to compare the math relationships, i.e., algebraically, numerically, and graphically.
Let us compare two functions numerically. Let us consider an example of y = 3x + 5. In this example, y is a dependent of x, so in other words, if we keep on changing the value of x, then y will increase as well. Let's look at the table as an example.
x, y = (-1, 2), (0, 5), (4, 17), (-5, -10)
Comparing functions graphically is probably the easiest to understand. You cannot always use this method because sometimes the inputs and outputs simply do not fit neatly on a coordinate plane. We compared the graph of two functions below:
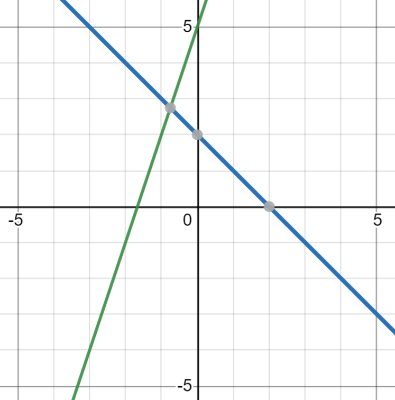
Can you spot any significant trends? Starting with the function represented by the blue line, we can clearly see that as the value of x increases, the value of y decreases. The function represented by the green line, on the other hand, has a much different trend. As the value of x increases, on the green line, so does the value of y. Graphs like this help us understand the nature of functions and make solid predictions of them.