Convert Rational Numbers to Decimals Worksheets
Having the ability to convert rational numbers in the form of proper fractions into decimal form is an important first step in many different types of financial transactions. When you go to borrow money in the form of a loan to buy something that you cannot afford now, but will be able to over time, the interest rate is most often stated in marketing materials in fractional form. To actually understand these interest rates, you will need to work these values into a calculator. To do that, you need to get them in decimal form. This collection of worksheets, lessons, and quizzes will help you learn how to do this quickly and accurately.
Aligned Standard: Grade 7 Number Systems - 7.NS.A.2d
- Conversion As Division Step-by-step Lesson- We have the problem already setup as a division problem for you to work with.
- Guided Lesson - We add a visual here in the second problem. Some students find this ultra helpful. Others have a bit of trouble with it.
- Guided Lesson Explanation - I give a verbal explanation for number two. Let me know if I should go further with it.
- Practice Worksheet - Time to work on mastering all three skills we present here.
- Matching Worksheet - I think you will really like how this one came out. I'm working on puzzles for this section now.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
The first and last sheet are what you commonly see in this section. The second sheet was based on a request.
- Homework 1 - Look at the first two digits. The first two digits are more than 11. Start with the first 2 digits. Divide the ones.
- Homework 2 - Use the grid to fill in the missing number.
- Homework 3 - Write 0.8 as a fraction in simplest form.
Practice Worksheets
I went off on a bit of a tangent with sheet 2, but I found that this skill is great to couple in here.
- Practice 1 - 3 columns are shaded. The column represents 3 tenths, or 0.3. 4 rows are shaded. The rows represent 4 tenths, or 0.4.
- Practice 2 - Find the sums of all the decimals.
- Practice 3 - More grids to get it going.
Math Skill Quizzes
You will find the second and third quiz to be a great summation for students.
- Quiz 1 - Write 0.17 as a fraction in simplest form.
- Quiz 2 - Convert a rational number to a decimal.
- Quiz 3 - Solve the decimal equation.
How to Convert Rational Numbers to Decimals?
Rational numbers are those numbers that can be written as a fraction; these can either be a proper fraction or an improper fraction. Proper fractions are those where the numerators are smaller than the denominators. Improper fractions are those where the numerators are greater than the denominators; these can also be represented as mixed numbers.
Rational numbers can easily be converted into decimals using a simple division strategy. A tip here that will help you in this conversion is the proper fractions are always less than one, while improper fractions are always greater than one. In the case of proper factions, just divide the numerator by the denominator and you will instantly create a decimal value. The problem comes as to where to draw the line for the decimal point. We will work through a problem together:
Convert 4/7 into a decimal. Your quotient value needs to be to the hundredths place.
Create a Division Problem: You create this by placing the numerator in the dividend position and placing the denominator in the position of the divisor. Place a decimal point, as a reference, directly after the dividend. You can see this setup below:
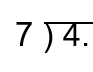
a) 7 is greater than 4, so it will not evenly go in at the ones place. We place a zero to indicate this.
b) 7 will go into 40, 5 times. We write the 5 at the tenths place of the quotient to indicate this and determine our remainder. We then continue on with this process until we get to the level of significance that we are wishing to achieve. The problem asks us to reach the hundredths place.
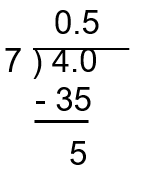
c) We now are left with a remainder of 50. 7 goes into 50, 9 times. We can continue on with the math from here, if we wish, but we were instructed to only go to the hundredths place, so our final answer is 4/7 in decimal form to the hundredths place, is 0.57.
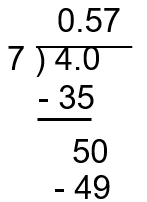
There are two types of decimals that you will run into when converting the rational values into decimals they are referred to as finite or terminating decimals and non-terminating decimals. The non-terminating form is considered to repeat on infinitely and is noted by the presence of three repeated dots (…) immediately after the decimal. Here are some examples of each for you to see:
1) Convert 3/4 into a decimal.
When you divide 3 by 4, you will get terminating decimal 0.75.
2) Convert 5/9 into a decimal.
When you divide 5 by 9 you will get a non-terminating decimal 0.555... This value indicates that the 5 at the thousandths place repeats on to all lower decimal values.