Naming Terms in Math Expressions Worksheets
There are many times when we will need to describe values that are found in an equation or expression. We can communicate this to other people with math symbols and numerical values, but we can also use the English language to achieve this. When we are doing this is formal way using language is often the norm. It may be because it seems more sophisticated or better packaged for a formal audience. Understanding all of the names that are attributed to parts of expressions is the foundational math vocabulary that you will need to use the English language to communicate these values. These worksheets and lessons help students learn how to master and understand all the terms found within an expression.
Aligned Standard: Grade 6 Expressions and Equations - 6.EE.A.2b
- Math Sentences In Words Step-by-step Lesson- Write the extended math sentence in words. This can be tricky!
- Guided Lesson - More work on this skill. I also throw up the concept of coefficients.
- Guided Lesson Explanation - If they have never seen coefficients, they will now!
- Practice Worksheet - More reps on the skills we are focused on in this unit.
- Variable Expressions Five Pack - Some of these are equations and some are expressions. Seemed like a good fit for this standard.
- Matching Worksheet - What's the value of coefficient "a" or something else.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
The vocabulary word "coefficient" stumps kids the most here.
- Homework 1 - What is the coefficient of x in the expression?
- Homework 2 - Example: (3 × 6) + 13 = Y
- Homework 3 - Which sentence best describes the equation?
Practice Worksheets
I would recommend that you do a full expression vocabulary lesson with students first.
- Practice 1 - Which sentence best describes: p = 24 + 54
- Practice 2 - Find the sentence that best explains: a = 33 + 14
- Practice 3 - What is the coefficient of x in each of the expressions?
Math Skill Quizzes
The skills get a little more difficult for each successive quiz here .
- Quiz 1 - The sum of seven and a number is five less than twenty two.
- Quiz 2 - Write the equation for: S is the difference of 17 and the quotient of 15 and 7.
- Quiz 3 - Write the equation for: R is the difference of 85 and the quotient of 44 and 11.
The Anatomy of Algebraic Expressions
Every algebraic expression is made up of terms that can be a constant, signed number, or variable. Terms are easy to spot because they are all the values that are not operators. They exist between, in front of, or behind these operation symbols. A constant is a number that does not change, its value is fixed. Variables are values that vary and are normally signified by the use of letter symbols (x, y). Coefficients are values that factors that are combined with a variable or variables. Some terms may have exponents attached to them. The exponent determines the degree of a term. If something is to the exponent of 4, it is said to have a degree of 4.
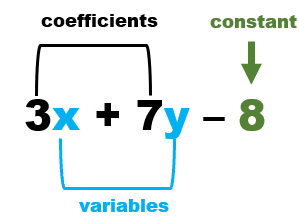
How to Write a Sentence that Describes the Equations?
An important step when solving a mathematical problem is to convert it into an algebraic math sentence that is easy to understand and contains all basic instructions to solve the problem. A lot of kids find it difficult to create these sentences to describe an equation, which becomes an obstacle when solving a number problem. The key to converting an equation into a sentence is to know the describing words for every arithmetic operation. The operators within an equation or expression make up the meat of math statement in words. This also explains the trajectory of statemen itself. Let’s examine each operation and what we know about it when used in math sentences:
Addition - You can use words such as total, altogether, sum, and more than to define the addition operations. You will find this operation low on the scale of the order of operations, so it is usually named towards the end of the sentence.
Subtraction - You can use the words such as: the difference between, less than, take away, remove by, and minus to define the subtraction operations.
Multiplication - You can use the terms: by, lots of, product and multiples to define the multiplication operation. You will also see set intervals named such as double, twice, and triple used for this operator.
Division - You can use the terms: divided, per, equally shared, grouped, quotient and dividend to define the division operation. The goal of using these words is express that some quantity or value is distributed equally across a fixed number of units.
Here is an example problem: Describe the equation: 4 ÷ (5 + 15) = z
Right away will key in on the operations that are taking place. There are two operations in this equation. 4 is being divided by the addition (sum) of 5 and 15. When we put all those values together, I that order, we create the variable z. If we put all this together, we can describe z as the quotient of 4 and the sum of 5 and 15. See! It is that easy!