Evaluating Algebraic Expressions Worksheets
Algebraic expressions are math phrases that are a combination of variables, constants, and operators. They are used to explain situations and understand all different types of systems and phenomena. Expressions consist of a series of mathematical terms that are separated by operators (+, -). There are three commonly found ways to classify algebra expressions based on the makeup of their terms. Monomials have only a single term, example: 3x, 4x2, 5xy. Binomials have two unlike terms meaning that they either have multiple variables or a variable and a constant, example: 2y + 4x, x +10. Polynomials are a real mixture of terms and consist of two or more terms. These worksheets and lessons will help students learn how to inspect expressions and learn to better understand and manipulate them.
Aligned Standard: Grade 6 Expressions and Equations - 6.EE.A.2a
- Writing Them Step-by-step Lesson- We give you an expression in sentence form and ask you to bring the integers to life.
- Guided Lesson - Explain the what is presented to you in word and numeric form. Tell us if the end value is classified as true or false.
- Guided Lesson Explanation - I spent a great deal of time on this one. See if it helps!
- Practice Worksheet - Write each expression in numeric form. What's with the lady bug?
- Matching Worksheet - Find a match between the numeric and sentence form of the expressions.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
You start by making sense of sentences and then you write your own expression sentences.
- Homework 1 - Write the following in number form: The difference of 75 and g.
- Homework 2 - The word "difference" indicates subtraction in the order that it is stated.
- Homework 3 - Observe the sign between the two integers above. It is a division symbol.
Practice Worksheets
I get a lot of people sending me compliments on these. Not sure why?
- Practice 1 - A quotient signifies the operation of division.
- Practice 2 - So this expression can be written as a quotient of x by 8.
- Practice 3 - Is (7 x y) an expression shown by words: The sum of 7 and y?
Math Skill Quizzes
The quizzes here are very clear cut and straight forward.
- Quiz 1 - Write the following in number form.
- Quiz 2 - Write the expression in number form: The sum of o and 3.
- Quiz 3 - State true or false : Is (56 - v) an expression shown by words: The difference of 56 and v.
Tips for Evaluating Algebraic Expressions
Though mathematics is all about numbers, the algebraic section of mathematics uses letters, words, and expressions to define a problem or model a scenario. In a given word problem, many words play a crucial role in deciphering the answer, but most times, it is challenging to determine the importance of certain words and expressions. Learning to assess what is going on in any math statement can help you move towards an answer quickly.
There are several commonalities that you find in any algebraic expression. They all consist of a mixture of numbers, variables, and at least one arithmetic operation. Let's look at all the fundamental parts of these math statements by look at all the parts of this specific example: 3x + 7y - 8. There are really three key aspects to this expression:
To restate the expression: 3x + 7y - 8
1) Constant - This is a number or value that does not change value. In this case it is 8.
2) Variable - These are symbols used represent a quantity that can be assumed to vary and capable of multiple values. In most cases, we use letters as the symbol for variables. In this case we have 2 variables: x and y.
3) Coefficients - This is the numerical multiplier of the variable(s). In this case, there are 2 because there are two variables: 3 and 7.
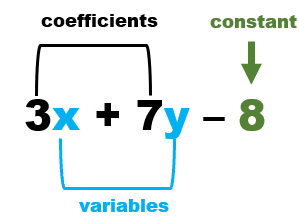
The diagram above shows the exact location of all these parts of an expression. It consists of 3 terms: 3x, 7y, and 8. A term is what is found between each operator symbol. Terms can be a variable, signed (+, -) number, or a constant.
Now that we understand the anatomy of an algebraic expression, how do we manipulate them and evaluate them? There are a series of fixed steps that you can take to break them down and make sense of them.
Step 1) Substitute Numbers for Variables - Replace the letters of expression with the assigned values. Most times you will evaluate a the fixed values that are given to you for each variable. The first step is to carefully replace the letters of expression with the values assigned by the problem. Now you have an math statement with only numbers in it. Write each value in parentheses.
Step 2) Perform the Given Operations - After substituting the values, now perform the operation in the correct order of the expression. Don't forget to use the correct order of operations.
Perform with exponents: Make sure that you consider the exponents too and perform correct mathematical operations.
Here's an example for you to work through:
2x2 - x + y, for x = 3 and y = -2.
2(3)2 - (3)+ (-2), 18 - 3 - 2
The answer is 13.