Multiply Multi Digit Whole Numbers Worksheets
Once students begin to advance past just multiplying single digit values, it becomes a great deal about staying organized. Of course, we encourage all teachers to review place values with students before moving forward to working with the products of multi digit numbers. Once they have a solid hang of what the value of each integer in a number signifies, they are ready to start multiplying multi digit numbers. We then teach them to find the product of the multiplier and multiplicand one place value at a time from right to left. The challenge is for them to remember the placeholder zeroes as they progress along with the problem. First, they will forget it entirely, then they will forget that the hundreds place has two zeroes, and the thousands has three. A few bumps and bruises and they’ll finally get it. This series of lessons and worksheets will help students learn how to multiply multi digit number properly.
Aligned Standard: Grade 5 Base Ten - 5.NBT.5
- Double and Triple Digits Step-by-step Lesson- Good old find the product problems. Vertically set out of course.
- Properties of Multiplication Step-by-step Lesson- I thought it was a good time to work this one out for you too.
- Guided Lesson - Horizontal and vertical multiplication mixed in with a bit of missing numbers math.
- Guided Lesson Explanation - Man, those vertical problems really take up space.
- Practice Worksheet - This one really pounds the skill into your brain.
- Matching Worksheet - Match the products with the problems they need to be in.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
The Xs denote the place holder of a zero in the example. I get asked that pretty often.
- Homework 1 - Two step problem walk through.
- Homework 2 - Use the box structure to your advantage.
- Homework 3 - There are several steps to these problems.
Practice Worksheets
I only put three problems on here to give you extra work space.
- Practice 1 - Keeping yourself organized is the key here.
- Practice 2 - Line up each movement of values.
- Practice 3 - Remember the value you need to attribute to the tens place.
Math Skill Quizzes
You will need some extra scrap paper for these quick quizzes.
- Quiz 1 - We introduce the thousands place here.
- Quiz 2 - Even bigger values can be found here.
- Quiz 3 - You may need extra scrap paper for this quiz.
What Are the Basic Rules of Multiplication?
Understanding mathematics is all about understanding the rules it entails. The course is filled with basic mathematical rules about each and every operation. This applies to all the rules, addition, subtraction, multiplication and division. However, there are a few more rules to follow in multiplication as it can make it much easier to solve problems quickly and accurately. If you are unaware of the basic rules to follow with multiplication operations, here we give you a run down on those.
So, what are the basic rules of multiplication?
1. Tables: The first and the foremost rule for multiplying numbers is to know your times tables. This is a series of single- and double-digit products that you can take time to memorize. Knowing tables can help you jump to the next step quickly.
2. Multiplication with 1: The number stays the same when multiplied by 1. Example: 20 x 1 = 20.
3. Multiplication with 0: Any number multiplied by zero, the result will be zero. Example: 22 x 0 = 0.
4. Double rule: It is important to remember these two special cases, when we are multiplying two numbers, we are actually doubling the number. For examples: 300 x 2 = 600
5. Order of Multipliers Doesn't Matter: Another rule to remember is that the order of numbers doesn't matter in multiplication. If you remember the commutative property of multiplication, you can place the factors in any sequence of your choice, the outcome will always be the same. You can multiply in order and the result will be the same regardless.
6. Add zeros: Any number multiplied by 10, 100 or 1000 you can simply add zeros to the end in the respective order. Example: 32 x 10 = 320, 27 x 100 = 2700 and 45 x 1,000 = 45,000
Remember to Use Placeholders When Multiplying Large Numbers
Once the problems you begin working on include a good number of place values, your accuracy in your answers will improve by simply organizing yourself. Long multiplication is a bit of a marathon. The first step is to make sure everything is aligned properly; each column should be on top of the other. Start by multiplying the ones place of the multiplier by the entire multiplicand. Once you get a value for the product of the ones place of the multiplier/multiplicand move to the tens place. Since we are multiplying by a tens place, we start our product with a zero in the ones place. This carries through the entirety of the problem. Signify the product with the proper number of zeroes as dictated by the place value of the multiplier.
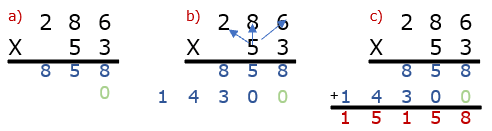
Example: 286 x 53
Step 1) Align the columns of the multiplicand and multiplier.
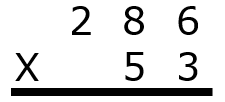
Step 2) Multiply the entire multiplicand (286) by the ones place (3) of the multiplier and place the product aligned below it.
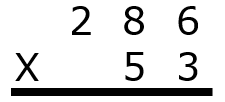
Step 3) Find the product of the tens place (50) of the multiplier by the multiplicand. a) Since this is a tens place value, we must put a placeholder zero in the ones place of our product. B) Process that product at the tens place. c) Find the sum of those values (858 + 1,430) to determine the total product (15,158).