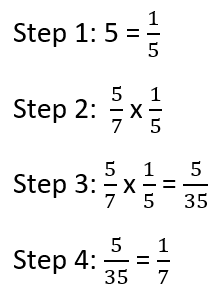Division of Fractions by Whole Numbers Word Problems Worksheets
We have done all different types of problems that have included fractions and whole numbers. We have explored all the different operations and how the two relate to one another through this entire process. When you consider these types of word problems you are really breaking a fraction apart into equal groups. In affect you are making it even smaller. If you end up working in construction, baking, chemistry, or anything that follows a basic recipe you will run into problems very similar to these on a regular basis. Below you find a series of worksheets and lessons to help you become familiar with word problems that require you to divide a fraction by a whole number.
Aligned Standard: Grade 5 Fractions - 5.NF.7
- Sharing Chocolate Pastries Step-by-step Lesson- How do you share a 1/4 pound of tasty bakery treat? Let's figure it out!
- Guided Lesson - A day in the kitchen, I guess! Math on scoops of ice cream, wafer biscuits, and dried fruit.
- Guided Lesson Explanation - As you could probably tell, I'm a huge fan of timelines.
- Practice Worksheet - Time to do a bunch of problems on your own without any prompts or pictures.
- Matching Worksheet - I know the units kind of give away the answers. At least you can see if the kids read well.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
You will find some real spatial problems in here that you might need to visualize in order to make sense of it.
- Homework 1 - Jett placed books evenly among 6 shelves. On one shelf he placed 8 books. How many books were there in total?
- Homework 2 - Sally had wallets. She gave the same number to 4 friends. One friend got 6 wallets. How many wallets were there in total?
- Homework 3 - Kayla equally distributed rings to 18 people. One person got 14 rings. How many rings were there in total?
Practice Worksheets
Is it called a "calligraphy" pen? I wasn't sure. I threw it through Google and there was no definitive answer anywhere.
- Practice 1 - Declan bought calligraphy pens. He distributed them evenly among 3 friends. One friend got 8 pens. How many calligraphy pens did Declan buy?
- Practice 2 - Anna distributed pairs of earrings to 18 friends. They all got the same amount. One friend got 4 pairs of earrings. How many pairs of earrings were there in total?
- Practice 3 - Sienna bought pen boxes. He distributed them evenly among 19 friends. One friend got 6 pen boxes. How many pen boxes did he buy?
Math Skill Quizzes
Denial seems to be a great Christmas gift giver. I always thought of her more as a taker. You'll see what I mean on number 1.
- Quiz 1 - Paige gave the same number of combs to 2 friends. One friend got 9 combs. How many combs were there in total?
- Quiz 2 - Gabriella equally distributed markers to 10 people. One person got 10 markers. How many markers were there in total?
- Quiz 3 - Harry bought magic balls. He distributed them evenly among 6 friends. One friend got 28 magic balls. How many magic balls did he buy?
How to Spot the Division of Fractions in a Word Problem
When you are tackling any story or situational based math problem your focus should be on identifying all the details first. Once you understand the overall process of what is happening, you just need to drop the numbers into the process to solve them. If we spot any of the following keywords, you bet the farm that division is taking place to solve the problem: average, cut, even, every, out of, ratio, share, and split. For example, if we were examining the problem: Jeanne was bought chocolates to share with her favorite teachers. If she purchased 3/4 pounds of chocolate and needed to share them between her 3 favorite teacher, how much chocolate would each teacher receive. The concept here is that an amount of chocolate will be shared between people (teachers). The word "share" tells us which operation we are working with. We are looking for the amount of chocolate each person would receive, if it were shared equally. If we were to write this as an equation it would resemble: amount of chocolate = all chocolate ÷ number of people. Like I said, we now just have to put the numbers in: amount of chocolate = 3/4 pounds ÷ 3. In the end each teacher would receive a quarter pound of chocolate.
How to Divide Fractions by Whole Numbers
A lot of kids find division to be a complex arithmetic operation and things get very complicated when division is turned up a notch to an advanced level where fractions get involved. Dividing fractions by whole numbers can get difficult but taking a step-by-step approach can help in countering the difficulties. Below we will talk you though it and then apply it to a full problem.
Step 1 - Convert the Whole Number into an Improper Fraction: You can always make a whole number a fraction by simply placing it over 1. This is pretty simple.
Step 2 -Flip the Divisor and Operation - Take the reciprocal of the divisor. That is the fraction that you are dividing by. When you do this, the division operation also gets countered and becomes a multiplication operation.
Step 3 - Multiply the Fractions - Multiply the numerator of both the fractions and multiply the denominators of both fractions. This will leave you with a final product.
Step 4 - Simplification – Note that this step is not always necessary, if the final value cannot be reduced further. You can test this by seeing if the numerator and denominator share a common factor. If they do, bring them to their simplest form.
Example: 5/7 ÷ 5.