• Andrew's Chocolate Step-by-step Lesson- Andrew shares some candy among his friends at his birthday party.
• Guided Lesson - Cold drinks at a New Year's party, grams of rice, and tennis balls. Just another day in the wonderful world of math.
• Guided Lesson Explanation - We show you how to setup those reciprocal based problems.
• Practice Worksheet - A nice solid mix of problems that give you a lot to think about.
• Matching Worksheet - Finally, quotients that come out to be whole numbers.

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

Some of these problems are truly challenging. I found myself triple checking the answers.

• Homework 1 - Richard bought a packet of wafers which is 1/6 of a pound. He fills 2 bowls with these wafers in equal amounts. What is the weight of each bowl?
• Homework 2 - Denise had 1/2 of a pound of cookies. She gave the cookies equally to her 2 daughters. How much did each daughter get?
• Homework 3 - Bailey made a 1/4 of a pound of donuts. He divided it equally into 2 pieces. What was the weight of each piece?

Practice Worksheets

I definitely encourage children to draw a picture when working on these problems.

• Practice 1 - Isabel had 1/6 of a pound of pastry. She has to divide it equally into 4 pieces. What was the weight of each piece of pastry?
• Practice 2 - Brett bought vermicelli that weighed 2/4 of a pound. He distributes the vermicelli into 5 bowls. What is the weight of each bowl?
• Practice 3 - Rose had 1/3 of a bowl of a hot chocolate. She gave that to her 4 friends. How much of the hot chocolate did each friend get?

Math Skill Quizzes

Again we see how the kitchen and math class meet again.

• Quiz 1 - Remo bought a muffin that weighed 1/6 of a pound. He distributes the muffin into 3 equal parts. What is the weight of each friend’s muffin?
• Quiz 2 - Joel had 1/5 of a bundle of candles. He gave it to his 3 friends. How much of the bundle did every friend get?
• Quiz 3 - Sienna had 1/3 of a pound of popcorn. She has to divide it equally among 7 bowls. What is the weight of each bowl of popcorn?

How to Divide Whole Numbers by Fractions

When you are dividing a whole number with a fraction, you are finding how many groups of the fraction can get fit in the whole. A basic method of dividing whole numbers by fractions is through multiplying the whole number with the reciprocal of the fraction or the inverted copy. This process is easier to understand when you work through a full problem. We will explore this strategy by solving the problem: 7 ÷ ¾

Step 1 : Make the Whole Number an Improper Fraction - You can convert any whole number to a fraction by simply placing it as the numerator over a denominator of 1. When we put this into work for us 7 becomes 7/1. Our problem now looks like this:

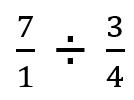
Step 2 : Flip the Division Sign to Multiplication While Taking the Reciprocal of Divisor - The divisor is the value that we are dividing by. In this case it is the second fraction (3/4). When we make the divisor a reciprocal, the operation (division) flips to the opposite operation (multiplication). The reciprocal is inverse of a term. So, for 3/4, it is going to be 4/3. Our problem now looks like this:

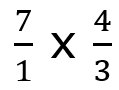
Step 3 : Multiply Fractions - Multiply the two fractions with each other. In order to multiply the fractions, first, you need to multiply the numerators with each other. You follow this by doing the same with the denominators. The product of these two fractions will be equivalent to the quotient of the division problem.

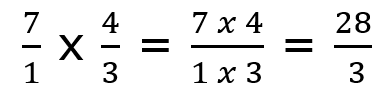
Step 4 : Reduce - Simplify the problem is possible. If you have an improper fraction, your teacher might require some change to the mixed number. Usually, the teacher will ask you to reduce the fraction to its lowest possible terms. In our case, there is no common denominator, but we can create a mixed number: 28/3 becomes 9 1/3.