Dividing Fractions Word Problems Worksheets
Identifying the need to divide in a story-based math problem is often difficult and almost cryptic at times. There is a solid strategy that you should begin to deploy and use regularly and this diagramming word problems. Start by identifying the variables, in most cases, those are the values or integers that are found in either number or word form. Circle these variables and any units that are attached to them. The second part of this strategy is essential, scan the problem for words and phrases that indicate an operation. In the problems on this page the variables will be mostly in fractional form. To spot the division operation the most commonly used terminology include: cut up, as much, equally shared, each group, half, parts, per, share. These lessons and worksheets will help you become comfortable with breaking down fraction division problems that are presented in word problems.
Aligned Standard: Grade 5 Fractions - 5.NF.7
- Tara's Licorice Step-by-step Lesson- How much licorice will each girl on the soccer team get?
- Guided Lesson - Slices of pizza, marbles in a bag, and a big old pile of receipts make for some great word problems.
- Guided Lesson Explanation - We work mostly to start with like fractions and then proceed from there.
- Practice Worksheet - I had to adjust the font to get it to be one printable page for you.
- Matching Worksheet - Match the quotient-based word problems to their final outcome.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
There are lots of problems that involve sweets here. I had a bit of sweet tooth that day (chocolate craving). When you hit 60, you'll understand!
- Homework 1 - Rosey has a box of chocolates. She has 3/8 of the chocolate in the box. She wants to share this box with her 3 friends. How much of the box will each friend get? You would approach this word problem by dividing 3 into the fraction.
- Homework 2 - Jasper bought 3/4 of a pound of cake. If his 2 children share this equally, how much will each child get? Students have difficulty when dividing fraction in half, but remember that it is the same thing as multiplying by one half.
- Homework 3 - Domino has a box that is 3/6 full of candies. He then evenly separated the box among 20 children. How much of the candies will each child get?
Practice Worksheets
I used to tackle these types of problems at dinner on Fridays when we have guests over. Especially when the conversation got a little stale or someone walked away for a bit. It usually make the math easy and take food last.
- Practice 1 - William has 2/3 of the goggles. He divides the goggles among 7 friends. How much of the goggles will each friend get?
- Practice 2 - Ella has 3/8 kg of baby corns. She wants to share the baby corns among 6 friends. How much of the baby corns will each friend get?
- Practice 3 - 10 people share 2/6 of a pound of the ice cream. How much of a pound of the ice cream will each person get?
Math Skill Quizzes
It is amazing how food and culinary type situations lend themselves to fraction-based math.
- Quiz 1 - Audrey made muffins for her children. She made 3/6 of a pack of muffins. She distributes the muffins equally among 5 children. How much of a pack of muffins will each child get?
- Quiz 2 - Zac bought a bag of sugar candy. He wants to share this bag with his 4 friends. The bag has 2/8 of a kg of sugar candies. How much of the sugar candy will each friend get?
- Quiz 3 - Chelsea has 5/7 of a box of candles. She wants to share the box among 6 friends. How much of the box will each friend get?
Tips on Dividing Fractions
Working with whole numbers is easy but getting familiar with the fractions and the operation between them is a bit more complicated. There are multiple methods of doing fraction division. Some people like will often work around fraction and skip to using a decimal format, but that will not work for all the problems that you with come across. I tend to find that students have the most success by using a simple three step process to easily divide fractions. We will work through an example of this strategy.
Example: ¾ ÷ ⅜
Step 1- Flip the Second Fraction: You will take the reciprocal of the second fraction (the divisor). This means that you replace the numerator with the denominator and vice versa.
In this case the divisor 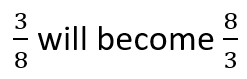
Step 2- Multiply the Fractions: Now that you have found the reciprocal of the division, you will multiply the fractions. If you remember back to fraction multiplication, you multiply the numerators together and the denominators together to form your product. Here is a walkthrough of this process:
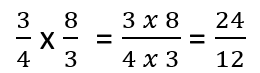
Step 3- Reduce: Note that you may not need to do this if it is already in the simplest form. You will simplify the numerator and denominator that goes on both equally. In our example 12 does just the trick, so this reduces to:
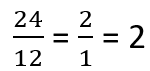
This is one of the quickest methods of dividing fractions. The top and bottom numbers are being multiplied with the same number. Since the number is the reciprocal of its bottom part, the bottom automatically becomes one. Dividing anything by one eventually leaves the value untouched and unchanged.