Estimating Angles Worksheets
Understand the spatial relationships that exist between various structures is a fundamental skill that will last with students well into adulthood. Having the ability to manage these thoughts well is a key skill in just about any type of construction-based project. Working up to that level all begins at the most simplistic level such as having the ability to estimate the amount of space that exist between two lines that form an angle. In this topic we explore how to best be able to estimate the distance that exists between these two angles. We show you how to estimate these angles in the lesson and at the bottom of this page. Students can use these worksheets to better understand angles and their role in geometry.
Aligned Standard: Grade 4 Measurement & Data - 4.MD.5
- Step-by-Step Lesson- We meet up with right angles to get this party started. They are the base of all else.
- Guided Lesson - A nice guesstimate activity. Remember to work with the standard guides.
- Guided Lesson Explanation - I like to explain these by making the angles relative to right edges and straight lines.
- Practice Worksheet - I really like to give kids this right after they start using a protractor. The standards list it first though.
- Matching Worksheet - Find the two matching angles. Beware they are all flipped around.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
We give some angles and ask you to estimate their measures. This is a great skill to have mastered.
- Homework 1 - What is the measure of this? Choose the best estimate.
- Homework 2 - This angle is about 1/9 the size of a right form. Work with that.
- Homework 3 - Use observational fractions to estimate bigger angles.
Practice Worksheets
More practice on guessing the measure of angles out of thin air.
- Practice 1 - What is the approximate measure of this angle?
- Practice 2 - You can also classify the name of them for bonus points.
- Practice 3 - Have another round of this for good luck.
Math Skill Quizzes
I made these all multiple choice so that scoring them would be much easier for you.
- Quiz 1 - Multiple choice for you. Read the angles and measures that you come across.
- Quiz 2 - Start by comparing each to a right angle.
- Quiz 3 - A little overlap can be found here.
How to Estimate the Measurement of an Angle
The easiest way to measure the angle you want to measure is through the use of a protractor. However, you will not always have a protractor at your disposal, and that can be a real issue for some students. Estimating measurements of an angle is much easier than what most students think. If you think of a 180° angle as a half a circle and understand a few measures in there everything falls into place and is much easier to handle. 180° angles are called straight. The straight form is the fundamental angle to understand and use. Every other major angle classification is built off of it. Here is a diagram of a straight version.
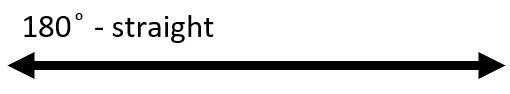
If you take that straight angle (180°) and cut it in half (90°) you form a right angle. Here is a diagram of a right form.
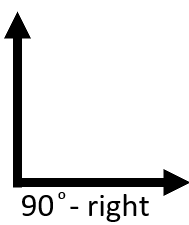
Now that we understand the 180° (straight) and 90° (right) angles everything else builds off of that. If an angle measures less than 90° , it is labelled as acute. It is good to understand the acute measure of half a right form which is 45°. This gives you a good reference to point to estimate the measure of all angles we come across, using this as a guide. Here is a visual diagram of the acute angle that measures 45°.
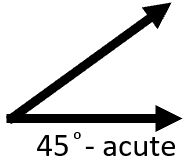
If an angle measures more than 90° , but less than 180° it is labelled as obtuse. It is good to understand the obtuse measure that is found half way between a straight and right form. which is 135°. This gives you a good reference to point to estimate to jump off of and work with. Here is a visual diagram of the obtuse angle that measures 135°.
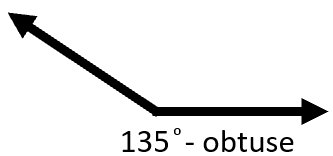
Estimating Measures in Triangles
You can estimate the angle of measurement using basic geometric principles that are used in triangles. For example, one of the basic principles of estimating a missing angle in a triangle is using the formula:
All angles of the triangle sum up to 180 degrees: a1 + a2 + a3 = 180°.
Using this formula, we can easily dictate the missing angle by putting in the other two values. For example:
∢ 1 = 56 degrees , ∢ 2 = 77 degrees, ∢ 3 =?
Formula: a1 + a2 + a3 = 180°
56 + 77 + a3 = 180°
a3 = 180 - 133°
a3 = 47°
Another basic geometric formula can be used for determining the missing angle in a circle. It is a basic mathematical principle that a circle is equal to 360 degrees. Hence, if a circle or a pie is divided into three equal pieces, and you only know the value of two angles, the remaining ∢ can easily be calculated.