Fraction to Decimal Notation Worksheets
Being able to name the same value in both decimal and fractional forms and understanding their relationship is strong skill to have as students advance further with math. It is important for students to understand that this is just a way to represent a value that is equivalent. There are many times that this conversion between notation makes sense. It is mostly when you need to perform a calculation that requires a certain operation. There are many real-world examples where entire industries have played with the concept of which is better to work with. The United States stock market prior to early 2001 listed all values in 1/16th fractional form. It was found that this notation discouraged people from taking part in trading. A collective of worksheets and lessons to help students learn how to convert fractions with denominators of tenths and hundredths to a decimal form.
Aligned Standard: Grade 4 Fractions - 4.NF.6
- Hundredths and Tenths Fraction to Decimals Step-by-Step Lesson- Convert six tenths and fifty-three hundredths to decimals.
- Guided Lesson - Convert fractions to decimals and then back again. Point to decimals on a numbers line.
- Guided Lesson Explanation - We show you how to take a quotient and turn into a decimal.
- Practice Worksheet - We work the skill from top to bottom and then flip it around once again.
- Compare and Order Decimals, Percents, and Fractions Five Worksheet Pack - All the usual suspects show up and you need to compare them.
- Matching Worksheet - Match decimals to their equivalent fractions.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
It is good to get students into the habit of dividing the numerator by the denominator. This really is used in all facets of math.
- Fraction to Decimals HW 1 - Fraction to decimal format is simply finding the quotient that the fraction represents.
- Decimals to Fractions HW 2 - We have a number in hundredths format. We can make it a whole number by multiplying both top and bottom by 100.
- Numbers Line HW 3 - 0.43 lies in between 0.4 to 0.5. So, we will put a line or circle in between 0.4 to 0.5 accordingly. Since it is closer to 0.4, the circle will be closer to it too.
Practice Worksheets
The first two sheets are your traditional fraction to decimal and vice versa. The third sheet is a numbers line, by popular request.
- Practice 1 - Write the following in fraction format.
- Practice 2 - Write the following in decimal format.
- Numbers Line Practice 3 - Where would 0.94 be on the numbers line below?
Math Skill Quizzes
Sorry, I couldn't have fit the numbers line into the quizzes as well. Just not enough room to work with!
- Quiz 1 - Write the following in fraction format.
- Quiz 2 - Write the following in decimal format.
- Quiz 3 - The be all end all for that next level.
How to Convert a Tenth or Hundredth Fraction to a Decimal
Place values play a crucial role in number systems, rounding off, and conversions. It is one of the fundamental concepts of mathematics. They can make a measurement more accurate and even win you a race. There is a unique value of every digit that is found in a number. Whether a digit lies before a decimal or after a decimal, each digit holds a unique value.
The smallest place values are found furthest to the right of any value. The largest place values are found to the left of any number. When decimal point is present the place value one to the right of the decimal point is called the tenths. If we move yet another place to the right, we reach the hundredths place.
Consider the fraction; 7/10, it is a tenth fraction. This means the value possess 7 parts of a total of 10 parts that makes up a whole value. When we make this a visual, we can show it as 7 shaded division our of 10 total divisions.
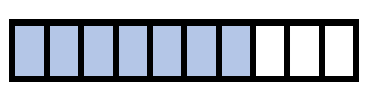
When we see that the numerator is smaller than denominator, we can say that the value of fraction is lower than one. Therefore, the number on the left side of the decimal can be written as 0. The fraction can be written in decimal form as 0.7.
Consider the fraction; 7/100, it's a hundredth fraction, which means out of the hundred divisions of a whole 7 parts are shaded. It can be visualized like this. The green represents the parts of the whole that the fraction possesses.
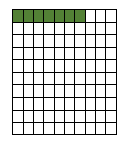
Similar to the above example, when the numerator is smaller than the denominator, the number is less than 1. We can write this fraction in decimal form as 0.07.
We can also turn this around and write decimals in fractional form. This is a bit easier, because all you need to do is determine the smallest place value represented by the far right non-zero number and place the entire value as the numerator over the value which that place represents. Let’s look at an example of both decimal places. Convert 0.4 and 0.56 to a fractional form.
Starting with the conversion of 0.4 we recognize that the lowest place is the tenths. We just place the value 4 as the numerator and the value 10 (tenths) as the denominator for a final fractional form of 4/10. Converting 0.56 is very similar. Identifying the last place as hundredths, we would place 56 as the numerator and the value 100 (hundredths) as the denominator for a final answer of 56/100.