Beginning Long Division Worksheets
When students begin to learn the math operation of division teachers usually present it in one of two ways (repeated subtraction or grouping/sharing) or both. This operation naturally flows well with the concept of repeated subtraction. For example, the simple equation 9 ÷ 3 = can be restated as how many times does it take you to subtract 3 from 9 until you have zero. You could also restate that equation from a sharing perspective in the form: 3 people would like to share 9 pieces of pizza equally. How many slices does each person get? Those techniques work great for single or single-double digit quotients, but what do you do when you are working with much larger numbers? Long division is a technique that can be used to divide larger numbers (normally 3 or more digits by 2 or more digits). It is all about determining if a divisor can go into a portion of a dividend and you sequential evaluate this until you reach a final solution. A detailed look at this strategy can be found in the lesson below. These worksheets are great when you are starting to learn long division.
Aligned Standard: Grade 4 Base Ten - 4.NBT.6
- Long Division Step-by-Step Lesson- We work on simple 2-3 step long division.
- Guided Lesson - Quotients are flying at you from every form. Word form, integers, and word problems.
- Guided Lesson Explanation - See if you like the way I spaced this one out. It made it a bit more logical for students.
- Practice Worksheet - Just like the guided lesson, we throw all types of division based questions at you.
- Division Word Problems 5-Pack - Good solid problems that all follow the same pattern to make sure you get it right.
- Matching Worksheet - Word formatted division problems for you to match the answers to.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
In the first two homeworks, I use the drawn arrow to help students follow the zeroes. I also have some quick division word problems to break it up.
- Arrows Down Homework 1 - A step by step example problem is provided for you.
- Using Arrows Homework 2 - This works through whole numbers without remainders.
- Word Problems Homework 3 - The cost of 60 chocolates is 180 cents. What is the cost one chocolate?
Practice Worksheets
I use a whole bunch of different formats here. This includes horizontal quotients, word based quotients, and stories.
- Horizontal Practice 1 - The problems are presented differently to you.
- Words Practice 2 - These are word based problems.
- Story Practice 3 - Lucas divided 228 by 19 on his scientific calculator. What quotient did the calculator display?
Math Skill Quizzes
I mixed all the different formats together to make one solid format.
- Quiz 1 - Nathan has 15 pairs of socks. The price of the socks is $45. Find the price of one pair?
- Quiz 2 - On a fuel station Hugo sell 200 liter fuel in a day and earn 750$. Find the price of 1 liter fuel.
- Quiz 3 - There are 6 members in a family. They share 24 bananas equally. How many bananas does each have?
What Is Long Division?
Division is a mathematical operation, also considered an opposite operation of multiplication. It is the process of splitting into equal parts or groups that results in fair or equitable sharing. For example, there are 15 cupcakes required to be divided among 3 friends. How can you share them equally? Divide 15 by 3, and you would learn that each friend would get 5 cupcakes.
But sometimes the numbers are complex and extensive. In such a situation, we commonly use a long division method to divide large or big numbers into parts and groups. These are division problems that you cannot do in your head. The long division helps in breaking down large and complex numbers into a sequence of steps that makes solving easier. Just like other division problems, there is a dividend, which is the large number divided by another number called the dividend — both these numbers divide to give a result quotient and, in many cases, a remainder.
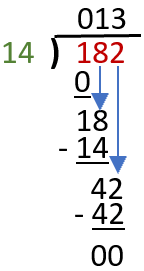
In the long division method, the splitting and grouping of dividends is the most important thing to make the problem easy to solve. Understanding this trick is basically the core principle of the long division method. Let's look at using this technique on the problem 182 ÷ 14:
Step 1: Define the dividend and divisor.
The dividend is the part that is being broken into parts. The divisor tells us how many parts the dividend is being broken into. In this case, the whole of 182 (dividend) is being broken into 14 (divisor) parts.
Step 2: Place them in proper quotient brackets.
Brackets help us keep track of this entire long division process much more accurately. The dividend is placed inside the bracket and the divisor is found outside the bracket.

Step 3: Work divisor into dividend sequentially.
a) We will work 14 into each digit of the dividend (182). We start by working 14 in the first digit (1). 1 ÷ 14 is 0 with a remainder of 14. You can just leave the remainder in place. We will place a 0 at the top of the bracket (start of your answer). We then multiply 0 by the divisor (14) and put the product inside the bracket.
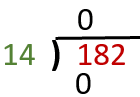
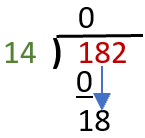
b) Draw a line under the zero that we just placed and subtract 0 from 1. This will allow us to bring down the 1 and the trailing number (8).
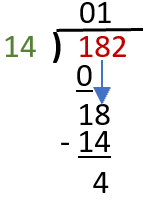
c) This allows us to move forward and divide 18 by the divisor (14). 18 ÷ 14 = 1 remainder 4. We write the 1 on top and show how the remainder 4 was created by subtracting 18 -14, as we have previously done.
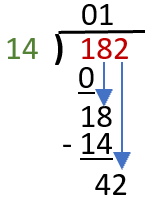
d) We then bring down the 2 as we have done previously. This allows us to find our final value by 42 ÷ 14 = 3. We write the 3 at the top of the bracket and subtract 42 from the bottom number to present our solution to this quotient. So, our final answer is 13.