Area of Squares Word Problems Worksheets
The concept of square footage is found in all walks of life. This is just the amount of flat space that is present in an area. This is a concept that you will want to master quickly before you start constructing just about anything these days. Students often get thrown by the term “square” in this. They think it can only be used for that fixed shape, but it can applied to all different types of shapes. The most important trick to learn is how to break large shapes into smaller pieces in order to help you calculate this measure quicker. It is simply the length of something times the width. These worksheets help students become comfortable with the concept of square footage and using these in word problems.
Aligned Standard: Grade 3 Measurement - 3.MD.6
- Square Area Step-by-step Lesson- Use rows and columns to determine the area of a rectangle.
- Guided Lesson - We have you draw area, partition a square, and find the area of a rectangle.
- Guided Lesson Explanation - There are many different ways of doing these problems. I show you the way that is logical to me.
- Practice Worksheet - This is more of a following directions activity than anything else.
- Matching Worksheet - Find the area of units within the rectangles.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Sheet one is a little more reading intensive than sheet two.
- Homework 1- Draw a rectangle made up of 3 rows and 4 columns. Determine the area of the rectangle.
- Homework 2- We can add up (count) the unit squares.
Practice Worksheets
These can also double as following directions worksheets.
- Practice 1- Color the shapes in the grid as indicated. Follow the directions in 2 and 3 to draw two additional shapes.
- Practice 2- Use the information provided to complete the missing parts of the table.
Math Skill Quizzes
The quiz focuses on solely the core skills needed.
- Quiz 1- Determine the unit square area of the figures below.
Why Is It Important to Understand the Concept of Area?
Area is a concept on mensuration, which holds significance in every-day mathematics. Its use is not just confined to solving mathematical word problems, but it can be used in daily life. It deals with two-dimensional shapes. It is defined as “the two-dimensional space an object occupies.”
Whether its farming, science or determining the size of the carpet you will have to use the concept of the area almost every day. Determining this value for two-dimensional shapes is easy to determine, especially for squares, rectangles, and triangles. The concept of the two-dimensional area has been in use since the time of the construction of pyramids of Giza.
The uses of calculating area in real-life includes purchasing tile for your bathroom or kitchen. When you purchase tile, you will need to calculate the area of the room. Depending on how long and wide a single tile is you will be able to understand how many tiles you will need for the room. When you are purchasing sod, you will need to calculate the size of the lawn to determine how much you will need to complete your lawn. There are numerous other situations where you will have to calculate the area to sort out the real-life problem. Many of them revolve around construction and building. When you first own a home, this is a skill you will want to remember.
Example; Your teacher asked you to decorate the classroom, and you need a lacey paper to cover the windows. You head to the shop but what do you ask the shopkeeper? A shopkeeper will ask you the size of the window so that they can provide you the right amount of paper. It is a situation where you will have to calculate the area. You go in your classroom, take a measuring tape, measure the length and the width of the window to calculate the area.
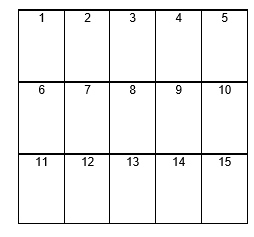
Example Area of Squares Word Problem
Partition the square below into 3 rows and 5 columns. How many squares are present after it is partitioned?

We will start this problem by following the directions and splitting the square into 3 rows (left to right) and then we break those rows into 5 columns (top to bottom). The image below illustrates the strategy that we just described.

The last portion of the problem asks us how many squares were created by creating those rows and columns. We can use simple multiplication (3 x 5) to determine that there are now 15 squares. We can also just count as you will see in the image below.