Working with Right Triangles Worksheets
This is the one of the geometric shapes that literally makes the construction of perfectly straight edges possible. Using the Pythagorean theorem, we can find missing sides of these shapes. As we advance into trigonometry, we will learn that you do not much information at all about these shapes to be able to determine all of the angles and lengths of sides. Something that people often do not realize is that if put a diagonal line across a rectangle and cut along that line, you have just created two right-angled triangles. Contractors use the property of geometry all day to create perfectly level and straight structures. This series of lessons and worksheets teach students how to complete figure out all measures on right triangles through a wide variety of techniques.
Aligned Standard: HSG-SRT.C.8
- Find Opposite Step-by-Step Lesson- Given two sides, find the third of the right triangle.
- Guided Lesson - In summer, I always think of problems in my head like number two.
- Guided Lesson Explanation - These problems real help students get the concepts that are mystifying to lower level geometry students.
- Practice Worksheet - This one took me a while. All nicely thought out real world problem set for you to work with.
- Matching Worksheet - In real life if you took the time to think and solve problems like this, you would need to find a hobby.
- Working with Right Triangles Worksheet Five Pack - All these problems have to visualized because they are in sentences.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
There are just so many different ways you can handle these problems.
- Homework 1 - A triangle contains exactly one 90° angle. The other two angles must total exactly 90 degrees. The famous Pythagoras Theorem defines the relationship between the three sides of a right triangle.
- Homework 2 - Jack saw a building that is 75 feet in height. The building casts a 30 foot shadow. What is the angle of elevation from the end of the shadow to the top of the building with respect to the ground?
- Homework 3 - A right triangle's opposite side is 10 and the hypotenuse is 18. Find the value of normal base?
Practice Worksheets
Over the course of the practice I show two different methods for answering the problems.
- Practice 1 - Find the value of normal opposite side?
- Practice 2 - Mark drives 10 km due east of his home. Then he heads 12km north. What is the total distance that he has travelled from his house?
- Practice 3 - Mr. Mike wants to purchase a square shaped table for his office. Table height is 6 feet. Mr. Mike ties a diagonal ribbon on the table. How long must be the ribbon?
Math Skill Quizzes
The first one is just with plain old triangles. The last two are all application word problems.
- Quiz 1 - A right triangle has a opposite side that is 10 units in length and a hypotenuse that is 14 units. Find the value of base?
- Quiz 2 - A road light is 40 feet in height and casts a shadow that is 15 feet long. What is the angle of elevation from the end of the shadow to the top of the road light with respect to the ground? This is assuming that the road light is 100% straight.
- Quiz 3 - Alan has a square shaped television. The height of television is 8 inches. Alan wants to put a diagonal paper on the television. How long must the paper be?
Tips for Working with Right Triangles
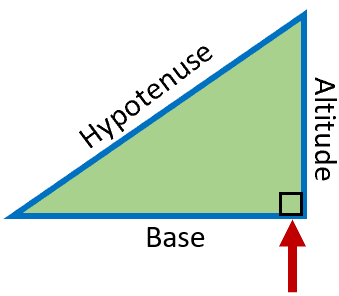
A right-angled triangle is one where one of the angles is 90 degrees. As you can see in the diagram to the right, that angle is often denoted by the presence of a square. There are a few unique features of these geometric shapes that you should be aware of. The longest side that is formed as a result of the right angle is opposite that right angle and called the hypotenuse. The altitude in a two-dimensional right triangle is the side that indicates height. The bottom side is referred to as the base. Depending on the orientation the two sides that are not the hypotenuse are interchangeable as result these sides are often referred to as legs. Since a triangle contains 180 degrees of internal angles, the sum of the measures of the legs must be 90 degrees.
The angles are often labeled which allows you to name the triangles. When naming triangles, we can pick any angle name them by labelling the angles in either a clockwise or counterclockwise direction. It does not which you pick as long as the angles fall in same consecutive order that they are found.
Working with right-angled triangles is relatively easier compared to other types of triangles. The reason behind this is simple. You always know the angles, and this can help solve many trigonometric word problems. One of the most common uses of right-angled triangles is the use of the Pythagoras theorem, which is Altitude2 + Base2 = Hypotenuse2. This allows you to find the measures of missing sides.
When working with right-angled triangles or solving problems that involve them, we can use the properties of sines, cosines, and tangents for determining many different missing sides or angles. Here are some other formulas that can be used with right-angled triangles to identify its unknown parts.
Sines: sin A = a/c, sin B = b/c | Cosines: cos A = b/c, cos B = a/c | Tangents: tan A = a/b, tan B = b/a
Let's just look at some of the cases where we don't know all the sides. Suppose we don't know the sides, but we are familiar with the other two sides. Using the Pythagoras theorem, we can easily identify the remaining two sides. If you know the measure of a side and angle, you can often determine all the others in this geometric environment which makes it a very handy shape to understand.
How Does This Apply to Real Life?
Understanding how to use and manipulate right triangles is one of the most important skills that covered in trigonometry. All of these geometric shapes consist of a single angle that measures ninety degrees. This allows use to use the Pythagorean theorem to our advantage to determine any unknown side or angle within the figure as long as we have a reference side or angle to work off of. In your everyday life you can use this to help achieve very similar things. The minute that you lean a ladder against a straight wall, you have created a right triangle. Want to know the height of the ladder, at what point it touches the wall, or the angle of the ladder, that can all be determined using the same exact math. You can use this math to determine the heights of building or natural structure in much the same way. When we are working with maps to locate areas or plot exact distances between objects, these figures can be pivotal to help you complete this. Anything that involves a coordinate system can be manipulated and better understood with the help of these figures. Mainly because if understand one measure you can learn a great deal about the system it is surrounded in.