Dividing Fractions with Unlike Denominators Worksheets
This operation between fractions is often intimidating to students when they first visit it but understand the basic principles will settle them down pretty quickly. I find that after about five practice problems students usually work out all the kinks. The first thing students need to be reminded is the basic vocabulary that define the part of a division problem. The dividend is the fraction that is being broken apart. The divisor is number of parts it is being broken into. The divisor is the value that we will take the reciprocal of, when dividing fraction. The quotient is the answer of the problem. Once they can identify those parts in these problems, this is not as challenging as it first appears. These worksheets and lessons help students learn how to divide fractions when they do not have the same denominator.
Aligned Standard: 5.NF.B.3
- Flip and Multiply Step-by-Step Lesson- Life would be great if we could make everything multiply at will, just like fractions.
- Guided Lesson - I threw a like fraction problem in here to make sure that students have the concept down entirely.
- Guided Lesson Explanation - There are steps to mathematical glory here.
- Horizontal Worksheet 5 Pack -Another big pack of numbers for you to work with.
- Practice Worksheet - Flip and multiply away in this series of problems pack.
- Matching Worksheet - Find the match for the quotients and the operations that created them.
- Division with Fractions and Mixed Numbers Practice - Another advanced set here. This really just adds one extra step for you to work with.
- Simple Mixed Number / Fraction Division Practice - Convert the mixed number and then start your division problem.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
I always like to remind students that when you divide fractions, "flip them and then cross them!"
- Homework 1 - Flip those integers around to get the party started. Then just go across the top.
- Homework 2 - Flip the second fraction. We start working with some thicker integers here.
- Homework 3 - Step two is to then multiply the first fraction by that flipped fraction.
Practice Worksheets
If kids are struggling with this skill, set them on these. They are a big help.
- Practice 1 - You should always end by simplifying the fraction. There are some rare cases where this is not required of you.
- Practice 2 - The first problem might make you roll over. That first problems reminds me of something.
- Practice 3 - You can alternatively flip the first fraction. If you want to get a little wild with it.
Math Skill Quizzes
Nothing too fancy here, just fraction quotients.
- Quiz 1 - See how well you understand this stuff here. Do not get carried away with those first few problems.
- Quiz 2 - Maintain the operations as you see fit. You will need to get in on this one.
- Quiz 3 - This is helpful when comparing droves of data. You can make a real difference with it.
How Do You Divide Fractions with Unlike Denominators?
Once you know the underlying principle, diving into unlike denominators becomes easy. We'll learn how to divide fractions with unlike denominators, look at what's common between dividing fractions with like and unlike denominators, and see how they're applied in the world. Some of you may be familiar with dividing fractions that have like denominators by simply cancelling out the denominators and dividing the numerators. Well, as it turns out, this rule for dividing fractions with like denominators actually comes from the rule for dividing fractions in general. That is, there is a rule for dividing fractions regardless of if their denominators are the same or not!
To divide fractions, we need to know how to multiply fractions. Thankfully, multiplying fractions is probably the easiest operation to perform on fractions. To multiply fractions, we simply multiply their numerators together and multiply their denominators together, then simplify. Well, the great news is that to divide fractions, we turn the division problem into a multiplication problem. To do this, we simply multiply the numerator of the division problem by the reciprocal of the denominator of the division problem.
There are two basic steps to follow when performing division between fractions.
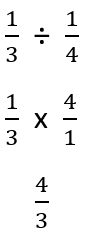
Step 1 - Take the reciprocal of the divisor. The reciprocal means to flip the fraction (switch the numerator and denominator). The divisor is normally second fraction or the fraction that appears after the division symbol.
Step 2 - Multiply those fractions and then simplify, if you need to.
Here is an example problem: ⅓ ÷ ¼
Step 1 - The divisor is 1/4. When we take the reciprocal of that fraction, we get 4/1.
Step 2 - When we multiply the numerator (1 x 4) we get 4 that serves as the numerator for our product. When we multiply the denominator (3 x 1) we get 3 that serves as the denominator for our product. We do not need to reduce the fraction further because there is not a common multiple found in the numerator or denominator.
Where Will You Run into Problems Like This in The Real World?
There are many times in your life in math class where you will not see the point to why you are learning something. In the case of fractions, unlike denominators often get you wondering where these kinds of things happen in everyday life. Fractions and cooking always go together. I cannot tell you how many different times I needed to convert a fraction to make them like, so that I could add or subtract them in a kitchen. If you ever get involved in a wood project, you will work with all different kinds of unlike values that you will need to make sense of. Keep that in mind the next time you would like to build a deck or just make a nice chair for yourself. When you start running or walking for distance, this will become a readily used skill for you.