Unit Circle Worksheets
The unit circle is a great tool to have handy when you are working with trigonometric functions. It will allow to solve problems that involve the functions sine, cosine, or tangent. It works in both units (degrees or radians) of angle measure. It is very helpful if you can memorize about 12 pieces of information about the table. If you can memorize the values for 30, 45, 60, and 90 degrees. There is a trick to it, most points just alternate between three values. Also, the quadrants have distinct positive and negative values for the ordered pairs. These worksheets and lessons help students understand the use of this tool and how it can be used in problem solving.
Aligned Standard: HSF-TF.A.2
- Hello Unit Circle Step-by-step Lesson - We examine how you can very quickly use the unit circle as a tool.
- Guided Lesson - We are all about conversions here.
- Guided Lesson Explanation - Most teachers will ask you to memorize the unit circle. I added a strategy in here for remember the main compass points.
- Practice Worksheet - Get a good bit more of practice in here. See how you can rework problems that you have already worked on.
- Matching Worksheet - See if you can get two matching values up in here.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
SOH CAH TOA CHO SHA CAO! Don't forget it.
- Homework 1 - Use the unit circle as a reference tool to solve problems.
- Homework 2 - The unit circle is a fundamental tool for architects and engineers.
- Homework 3 - These types of problems are often related to determining and predicting heights and distances.
Practice Worksheets
If the above acronym is foreign to you? You might want to do a little review first.
- Practice 1 - Find the value of a given trigonometric ratio using unit circles: cos Θ =, tan Θ =, sec Θ =, csc Θ =
- Practice 2 - This type of trig. math is often used in mapping and geographic applications.
- Practice 3 - Computer Aided Design (CAD) programs often are rooted in the use of this.
Math Skill Quizzes
Having a full unit circle handy is a must for some careers. Engineers are high-fiving right now.
- Quiz 1 - We will determine a variety of ratios.
- Quiz 2 - Trig. ratios are commonly used in astronomy.
- Quiz 3 - The movement of light is often predicted in a similar manner.
What is the Unit Circle?
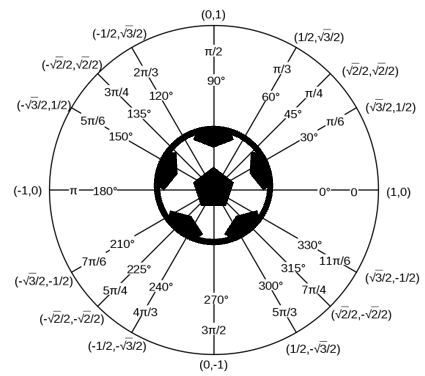
A circle with a radius of 1 is known as a unit circle. In simple terms, the distance from the center of the circle to any part of the edge of the circle is 1. The most significant thing about this tool is that calculations and equations are made simpler by using it because they are all based on a simple measure. If you take a look to the right, you will see a soccer ball surrounded by the unit circle. The center of the circle is always located at the origin where the x and y axis meet.
It is also useful in learning more about angles and lengths. Suppose that the center of the circle is present at the center of the coordinate system with the y-axis going vertically and x-axis going horizontally. The circle intersects the x-axis at y = 0 and x = 1. The angle at this point moves in the counterclockwise direction. Hence, at the point y = 0 and x = 1 the circle has an angle of zero degrees.
The unit circle has a circumference of 2Π . So every quadrant holds a measure of Π/2. This makes it easier to determine the length of arcs. The arc of it measures the same as the central angle that intercepts the arc. Also, because the radius is one, we can directly estimate trigonometric functions (sine, cosine and tangent) from the unit circle. When you apply the Pythagorean theorem to a unit circle, you spot all of the functions with ease. What makes this thing so helpful is that it lets you easily calculate the trigonometric function (cos, sin, and tangent) of any angle along the entire circle.
When Will You Use This?
As we stated at the start of this topic, this tool makes it a cinch to solve for the cosine, sine, or tangent of any degree/radian. You will see that some composition notebooks provide this as a reference tool. By the time you have reached this skill, you should a solid understanding of Pythagorean theorem and calculating the measures within a triangle. As we know, the sum of all the angles within a triangle are 180 degrees. Where the unit circle catches stride is for measures that are greater 180 degrees. This tool applies to the simplest pleasures of our life, like buying a pizza. Some students may not know this, but our standard pizzas are cut with exactly four cuts to create exactly eight slices. If the unit circle was followed, each of those eight slices will be the same exact size. Sonar technology is a direct application of this tool. A sonar ping is sent out in a circular path from where it originated, any disruptions within their path indicate an object of some type. Guess how they pinpoint exactly where that object is and gauge the size of it? You guessed it!