Graphing Exponential and Logarithmic Functions Worksheets
When we graph functions of any type, they all have their unique features. As you see them more, if you may see the graph of a function before seeing the actually function, you will quickly be able to realize the equation of the function. Graphs of exponential function resemble a bit of a boomerang. Where it slight rises across the y axis as the x values increase. Logarithm functions are inverses of exponential functions, so when you plot them on the graph you get a boomerang that looks upside down. These lessons and worksheets show students how to graph these two common functions that are the inverse of one another.
Aligned Standard: HSF-IF.C.7e
- Differential Exponent Graph Step-by-step Lesson- This graph was a slight challenge for me when I first came across these problems again.
- Guided Lesson - You will come across one exponent and two logarithmic.
- Guided Lesson Explanation - See if these follow the general rules to help it make more sense for you.
- Practice Worksheet - By the time students get to number six, they should have a solid understanding of how to get this all rolling.
- Matching Worksheet - Match the lettered values to the tables and graphs; that does make it easier.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
Understanding how negative values affect the graphs are key.
- Homework 1 - Since 4-x is zero when x=4, we will choose x values around 4 in our table of values.
- Homework 2 - We can graph x= 4y by using the same method for exponential functions, except this time we will choose values for y and then compute the corresponding values for x.
- Homework 3 - Graph f(x) = 67-x : At first looks like 6x should reflect across the y-axis since x is negative. However, the graph tells a different story.
Practice Worksheets
Time to start understanding the concept of function comparisons. What happens if you change one variable?
- Practice 1 - Rewriting f(x) =y= log11x in exponential form we get x= 11y.
- Practice 2 - Graph f(x) = 41-x
- Practice 3 - Rewite all the problems first, it will make it faster for you.
Math Skill Quizzes
We did pack a lot of questions into these sheets.
- Quiz 1 - Many more graphs for you with a ton of hints.
- Quiz 2 - Eight graphs for you to get after.
- Quiz 3 - The exponents can be difficult on this one.
How to Graph Exponential and Logarithmic Functions
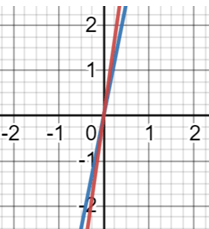
Exponential and logarithm functions are essential aspects in the field of mathematics. Given that on a theoretical basis, both of them are inversely proportional to each other. Here, let us look at the procedure to construct graphs of both these functions and their relativity with each other.
Exponential Function - The exponential function is much easier to work with, so let’s start there. These functions have an unknown variable that is an exponent rather than the base. Let us consider an example of the function, f(x)= 5x and f(x)= 7x. Now, whatever the value of x, it will increase or decrease in terms of 5 and 7. Look at the graph and the values presented below on the function. x, f(x)= 5x, f(x)= 7x : 0, 1, 1 | 1, 5, 7 | 2, 25, 49 | 3, 125, 343 | 4, 625, 2401 | 5, 3125, 16807. The blue line indicates the graph of f(x) = 5x and the red line depicts f(x) = 7x.
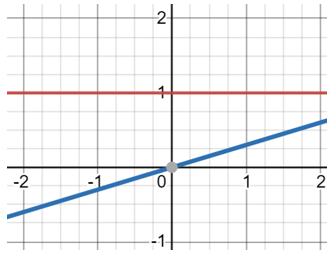
Logarithmic Function - By definition, the logarithmic function is an equation that consists of the independent variable which occurs in the form of the logarithm. Close values of the function create asymptotic graphs that approach arbitrarily close to each other. Let us consider an example with the functions f(x) = log2x and f(x)=log10x. x, f(x)=log2x, f(x)= log10 . Just like any other equation we pick set values for x and plug them into the function to generate values for y (f(x)). We then take these ordered pairs that we have created and plot them on the graph. Looking at the graph, the blue line depicts the equation f(x) = log2x and the red line indicates f(x) = log(10).