• Math Sentences as Algebraic Expressions Lesson - When we are translating a math sentence, it is often helpful to write the values in number form to help make sense of them. Let us do that to this sentence. We will rewrite the sentence and point out any figures that make themselves apparent. We will highlight the word values with colors as well.
• Guided Lesson - Write this math statement as an algebraic expression: The sum of one half of an unknown value and three times itself.
• Guided Lesson Explanation - I like to approach expressions by breaking them down into smaller pieces and describing each operation and value. Then I come back and describe how all of the components interact.
• Practice Worksheet 1 - You start with math phrases and you give them some mathematical form.
• Practice Worksheet 2 - Very similar to the previous sheet, but it gives you multiple variables with each sentence.

• Answer Keys - These are for all the unlocked materials above.

Homework Sheets

You will be given statements that are math based and written in word form. Your job is to bring the math alive.

• Homework 1 - You will work on sentences like: The answer of some number divided by four added to the same number squared.
• Homework 2 - See if you can make sense of this statement: The product of three and a number plus the product of five and another number is greater than twenty.
• Homework 3 - Bring more of these sentences to life in math form.
• Homework 4 - Write each phrase in algebraic form.
• Homework 5 - This are a bit more difficult

Practice Worksheets

We start to shift our focus away from the numbers and really have to get a hold of what symbols start us off on our path.

• Practice 1 - We use a unique approach to these problems like: One half of a number plus one third of another number.
• Practice 2 - I would approach these step by step and see what you can pull from every phrase that presents itself.
• Practice 3 - I like to write the values indicate first and then arrange them to fit the expression.
• Practice 4 - These are a little bit more difficult. Here is an example: Twice x squared divided by the product of 5 and x cubed is less than y.

Math Skill Quizzes

Make the math jump from the sentence to score high marks with this one.

• Quiz 1 - This is a very simple one for students who are having difficulty.
• Quiz 2 - These problems are vastly more complex than what we have seen previously.
• Quiz 3 - The level of complexity gets amped up here really quickly.
• Quiz 4 - This is the most difficult of the bunch.

Parts of Algebraic Expressions

Algebraic expressions are really helpful to model common real-world problems where we do not value know a value for certain. The uncertain values are modelled through the use of things that are called variables. Variables are often stated explicitly through the use of letters of the alphabet. The two variables that you are probably most familiar with are (x and y). In order to make complete use of them, we need to understand all the moving parts of these expressions.

Algebraic expressions are a combination of several things usually numbers, variables, and at least one operator (+, -, ×, ÷). In front of the variables, you will often find coefficients that multiply the value of the variable. Constants are fixed numbers that do not change value. When we reflect back on these expressions, we can break each part up into terms which individual variables, variables coupled with multipliers, and constants. Terms are what are found between the operators. When terms possess the same variable, they are called like terms and can be combined. For example, 4x and 2x. Take a look at the parts of this expression and see how we label all the parts:

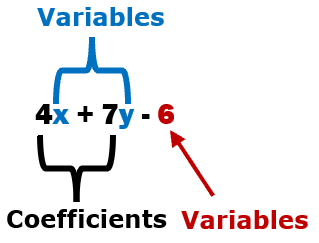
4x + 7y - 6

The coefficients are (4 and 7).

The variables that are present are x and y.

The constant present is 6.

It is composed of 3 terms: 4x, 7y, and 6.