Multiplying and Dividing Rational Expressions Worksheets
Students get deeper into algebra and often forgot that a large amount of the curriculum is just a slight advancement from what they learned in middle school. This is obviously one of those circumstances. We need to remind ourselves that rationale expressions when we take a step back present just as a fraction. Due to that extension, you can process division and multiplication operations of rationale expression just as if they were fraction. Another thing to remember is that the division of a set of fractions is the same thing as multiplication you just need to take the reciprocal of the divisor first. This selection of worksheets and lessons teach students how to find products and quotients of a set of rational expressions.
Aligned Standard: HSA-APR.D.7
- Dividing Complex Expressions Step-by-step Lesson- When I first saw this type of problem as a kid, I remember think that I'm not in Kansas anymore. This is the big time!
- Guided Lesson - You will find multiplication and division spread across these problems.
- Guided Lesson Explanation - Step one is always to get everything in the same form. With this skill it will require placing a one above or below the current value.
- Practice Worksheet - I tried to give you enough space to write on the paper with these problems. Most kids feel that it is adequate room for them.
- Matching Worksheet - Match the operations to the final value after performing all the operations required to simplified.
- Answer Keys - These are for all the unlocked materials above.
Homework Sheets
I find this is one of those standards that kids either get on their first try or they need constant remediation on it.
- Homework 1 - To divide by a fraction, multiply by its reciprocal.
- Homework 2 - Rewrite the second expression as a fraction.
- Homework 3 - To divide, multiply by the reciprocal.
Practice Worksheets
See if you like how I fit the operations in there for these.
- Practice 1 - Multiply the numerators and multiply the denominators.
- Practice 2 - Divide and simplify your answer.
- Practice 3 - Watch out for all the extra operations here.
Math Skill Quizzes
I wrote individual directions for each problem to help students focus on their goal for each problem.
- Quiz 1 - Divide. Write your answer in simplest form. Remember to evaluate the terms to see if you can reduce the terms.
- Quiz 2 - There are sections will double division here. We get more advanced with this skill.
- Quiz 3 - More division in this quiz. You are asked to reduce as far as you can.
How to Multiply and Divide Rational Expressions
Rational numbers are always tricky to solve because the present as fractions. Multiplication and division are two of the most basic operations in rational expressions.
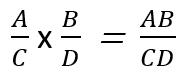
Multiplication - This is very similar to straight up fraction multiplication. The first thing you need to do is ensure that none of the denominators are equal to zero. The next step is to see if you can factor both the numerator and denominator. Then we can write them as a single fraction. You do this by presenting both numerators and denominators as a product of one another. It would follow the form that is presented to the right. All that you would need to do is to simplify the rational expressions and evaluate them.
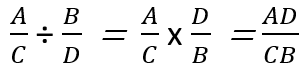
Division - Division of these expressions does follow suit and present just like a fraction on a grander scale. The first thing we do is take the reciprocal of the second fraction. That means to switch the positions of the numerator and denominator. Now we treat it just like we did when processing the multiplication operation. You simply multiply the rational expressions. So, we try to learn that by using an example. For example, how would you go about simplifying this:
(8 - K) / (K2 - 64) ÷ (K - 8) / (K + 8)
So, whenever we have fractions divided by another fraction, we leave the first one alone and flip the second fraction as the division will now be converted into multiply.
(8 - K) / (K2 - 64) x (K + 8) / (K - 8)
If we pay close attention, we can see that the two factors have opposite signs in their numerators and denominators.
If we take "-" common from 8 - K, we get: (K - 8) / (K2 - 64) x (K + 8) / (K - 8)
Using the rule of cross-multiplication we can cancel out K - 8. Also, we can expand K2 - 64. - (K + 8) / (K + 8) (K - 8) x (K + 8) / (K - 8)
Remainder: -1 / K - 8
Tips for Solving These Types Problems
A rational expression is a fractional math statement where either a numerator or denominator or both are polynomials. As we reviewed above, when you multiply these guys you treat them just like basic fractions which means that you find the product of the numerators and then you find the product of denominators. When finding the quotient of these expressions we use the same technique as multiplication, but before we do you turn the second fraction upside down (take the reciprocal). There are two trains of thought when performing these operations and it all revolves around when to simplify the fractions. I find that have mixed opinions on when you should reduce the fractions. Some teachers profess that you always start by reducing, other will understand this method, but have a slightly different take on it. Rather than reducing at the finish, they take a more case by case approach. If can see some operations that can be performed on the starting values, why fix what is not broken? The best summation of this method is to review the starting values and then go from there. If the values are hard to work with because they are large, then it is time to reduce before performing any operations. As you get more advanced, you may be confronted with large multi-term polynomials and quadratic expressions. In those cases you will need to factor the polynomials and locate common factors.